Teach yourself statistics

Hypothesis Test for Regression Slope
This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y .
The test focuses on the slope of the regression line
Y = Β 0 + Β 1 X
where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of the independent variable, and Y is the value of the dependent variable.
If we find that the slope of the regression line is significantly different from zero, we will conclude that there is a significant relationship between the independent and dependent variables.
Test Requirements
The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.
- The dependent variable Y has a linear relationship to the independent variable X .
- For each value of X, the probability distribution of Y has the same standard deviation σ.
- The Y values are independent.
- The Y values are roughly normally distributed (i.e., symmetric and unimodal ). A little skewness is ok if the sample size is large.
The test procedure consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
State the Hypotheses
If there is a significant linear relationship between the independent variable X and the dependent variable Y , the slope will not equal zero.
H o : Β 1 = 0
H a : Β 1 ≠ 0
The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.
Formulate an Analysis Plan
The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.
- Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
- Test method. Use a linear regression t-test (described in the next section) to determine whether the slope of the regression line differs significantly from zero.
Analyze Sample Data
Using sample data, find the standard error of the slope, the slope of the regression line, the degrees of freedom, the test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.
| Predictor | Coef | SE Coef | T | P |
| Constant | 76 | 30 | 2.53 | 0.01 |
| X | 35 | 20 | 1.75 | 0.04 |
SE = s b 1 = sqrt [ Σ(y i - ŷ i ) 2 / (n - 2) ] / sqrt [ Σ(x i - x ) 2 ]
- Slope. Like the standard error, the slope of the regression line will be provided by most statistics software packages. In the hypothetical output above, the slope is equal to 35.
t = b 1 / SE
- P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.
Interpret Results
If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.
Test Your Understanding
The local utility company surveys 101 randomly selected customers. For each survey participant, the company collects the following: annual electric bill (in dollars) and home size (in square feet). Output from a regression analysis appears below.
|
Annual bill = 0.55 * Home size + 15 | ||||
| Predictor | Coef | SE Coef | T | P |
| Constant | 15 | 3 | 5.0 | 0.00 |
| Home size | 0.55 | 0.24 | 2.29 | 0.01 |
Is there a significant linear relationship between annual bill and home size? Use a 0.05 level of significance.
The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:
H o : The slope of the regression line is equal to zero.
H a : The slope of the regression line is not equal to zero.
- Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a linear regression t-test to determine whether the slope of the regression line differs significantly from zero.
We get the slope (b 1 ) and the standard error (SE) from the regression output.
b 1 = 0.55 SE = 0.24
We compute the degrees of freedom and the t statistic, using the following equations.
DF = n - 2 = 101 - 2 = 99
t = b 1 /SE = 0.55/0.24 = 2.29
where DF is the degrees of freedom, n is the number of observations in the sample, b 1 is the slope of the regression line, and SE is the standard error of the slope.
- Interpret results . Since the P-value (0.0242) is less than the significance level (0.05), we cannot accept the null hypothesis.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Linear Regression Equation Explained
By Jim Frost 4 Comments
A linear regression equation describes the relationship between the independent variables (IVs) and the dependent variable (DV). It can also predict new values of the DV for the IV values you specify.
In this post, we’ll explore the various parts of the regression line equation and understand how to interpret it using an example.
I’ll mainly look at simple regression, which has only one independent variable. These models are easy to graph, and we can more intuitively understand the linear regression equation.
Related post : Independent and Dependent Variables
Deriving the Linear Regression Equation
Least squares regression produces a linear regression equation, providing your key results all in one place. How does the regression procedure calculate the equation?
The process is complex, and analysts always use software to fit the models. For this post, I’ll show you the general process.
Consider this height and weight dataset. There is clearly a relationship between these two variables. But how would you draw the best line to represent it mathematically?

Regression analysis draws a line through these points that minimizes their overall distance from the line. More specifically, least squares regression minimizes the sum of the squared differences between the data points and the line, which statisticians call the sum of squared errors (SSE).
To learn how least squares regression calculates the coefficients and y-intercept with a worked example, read my post Least Squares Regression: Definition, Formulas & Example .
Let’s fit the model!
Now, we can see the line and its corresponding linear regression equation, which I’ve circled.

This graph shows the observations with a line representing the regression model. Following the practice in statistics, the Y-axis (vertical) displays the dependent variable, weight. The X-axis (horizontal) shows the independent variable, which is height.
The line is also known as the fitted line, and it produces a smaller SSE than any other line you can draw through these observations.
Like all lines you’ve studied in algebra, you can describe them with an equation. For this analysis, we call it the equation for the regression line. So, let’s quickly revisit algebra!
Learn more about the X and Y Axis .
Equation for a Line
Think back to algebra and the equation for a line: y = mx + b.
In the equation for a line,
- Y = the vertical value.
- M = slope (rise/run).
- X = the horizontal value.
- B = the value of Y when X = 0 (i.e., y-intercept).

So, if the slope is 3, then as X increases by 1, Y increases by 1 X 3 = 3. Conversely, if the slope is -3, then Y decreases as X increases. Consequently, you need to know both the sign and the value to understand the direction of the line and how steeply it rises or falls. Higher absolute values correspond to steeper slopes.
B is the Y-intercept. It tells you the value of Y for the line as it crosses the Y-axis, as indicated by the red dot below.

Using the intercept and slope together allows you to calculate any point on a line. The example below displays lines for two equations.

If you need a refresher, read my Guide to the Slope Intercept Form of Linear Equations .
Applying these Ideas to a Linear Regression Equation
A regression line equation uses the same ideas. Here’s how the regression concepts correspond to algebra:
- Y-axis represents values of the dependent variable.
- X-axis represents values of the independent variable.
- Sign of coefficient indicates whether the relationship is positive or negative.
- Coefficient value is the slope.
- Constant or Y-intercept is B.
In regression analysis, the procedure estimates the best values for the constant and coefficients. Typically, regression models switch the order of terms in the equation compared to algebra by displaying the constant first and then the coefficients. It also uses different notation, as shown below for simple regression.
Using this notation, β 0 is the constant, while β 1 is the coefficient for X. Multiple regression just adds more β k X k terms to the equation up to K independent variables (Xs).
On the fitted line plots below, I’ve circle portions of the linear regression equation to identify its components.
Coefficient = Slope
Visually, the fitted line has a positive slope corresponding to the positive coefficient sign we obtained earlier. The slope of the line equals the +106.5 coefficient that I circled in the equation for the regression line. This coefficient indicates how much mean weight increases as we increase height by one unit.

Constant = Y-intercept
You’ll notice that the previous graph doesn’t display the regression line crossing the Y-axis. The constant is so negative that the default axes settings don’t show it. I’ve adjusted the axes in the chart below to include the y-intercept and illustrate the constant more clearly.

If you extend the regression line downwards until it reaches the Y-axis, you’ll find that the y-intercept value is -114.3—just as the equation indicates.
Interpreting the Regression Line Equation
Let’s combine all these parts of a linear regression equation and see how to interpret them.
- Coefficient signs: Indicates whether the dependent variable increases (+) or decreases (-) as the IV increases.
- Coefficient values: Represents the average change in the DV given a one-unit increase in the IV.
- Constant: Value of the DV when the IV equals zero.
Next, we’ll apply that to the linear regression equation from our model.
Weight kg = -114.3 + 106.5 Height M
The coefficient sign is positive, meaning that weight tends to increase as height increases. Additionally, the coefficient is 106.5. This value indicates that if you increase height by 1m, weight increases by an average of 106.5kg. However, our data have a range of only 0.4M. So, we can’t use a full meter but a proportion of one. For example, with an additional 0.1m, you’d expect a 10.65kg increase.
Learn more about How to Interpret Coefficients and Their P-Values .
For our model, the constant in the linear regression equation technically indicates the mean weight is -114.3kg when height equals zero. However, that doesn’t make intuitive sense, especially because we have a negative constant. A negative weight? How do we explain that?
Notice in the graph that the data are far from the y-axis. Our model doesn’t apply to that region. You can only interpret the model for your data’s observation space.
Hence, we can’t interpret the constant for our model, which is fairly typical in regression analysis for multiple reasons. Learn more about that by reading about The Constant in Regression Analysis .
Using a Linear Regression Equation for Predictions
You can enter values for the independent variables in a regression line equation to predict the mean of the dependent variable. For our model, we can enter a height to predict the average weight.
A couple of caveats. The equation only applies to the range of the data. So, we need to stick with heights between 1.3 – 1.7m. Also, the data are for pre-teen girls. Consequently, the regression model is valid only for that population .
With that in mind, let’s calculate the mean height for a girl who is 1.6m tall by entering that value into our linear regression equation:
Weight kg = 114.3 + 106.5 * 1.6 = 56.1.
The average weight for someone 1.6m tall in this population is 56.1kg. On the chart below, notice how the line passes through this point (1.6, 56.1). Also, note that you’ll see data points above and below the line. The prediction gives the average, but that range of data points represents the prediction’s precision.

Learn more about Using Regression to Make Predictions .
When you know how to interpret a linear regression equation, you gain valuable insights into the model. However, for your conclusions to be trustworthy, be sure that you satisfy the least squares regression assumptions .
Share this:

Reader Interactions
July 17, 2024 at 11:20 am
Thanks so much. Really helpful.
May 25, 2023 at 1:20 pm
Hello Jim, first of all, I have to say, it is a pleasure to read your books! I’m focused on the linear relationship and the different statistical tests, interpretation etc. The final goal is a paper concerning the estimation of investments in the area of plant construction, on the basis of historical data and a recommended non- linear relationship. (y=X^n) The accuracy of the mathematical model will be described with a confidence interval for the expected values and a prediction interval for individuals. An addition interesting point is the calculation of a prediction interval for future observations. My question based on a book which describes the confidence interval of a linear relationship for the expected values as a linear function! This is contrary to my understanding, statistic books and the law of large numbers. I would greatly appreciate to get an information with regard to that discrepancy. Best wishes from Germany and thank you in advance Klaus
January 29, 2023 at 11:24 am
I was searching during last 4 days for regression calculation & interpretation, I’ve learnt a lot. Still I’m searching to interpret the calculated data by MINITAB.
October 29, 2022 at 4:59 pm
Wondering what regression (or other) test we would run if we had a research question that looked at somethin like : does work out intensity (low, medium, high) and self reporting of sleep quality (good vs. bad) – our independent variables – affect the BMI % of respondents (where BMI % will be our dependent variable). Would multiple regression be the appropriate test? Multiple discriminant analysis perhaps? MANOVA?
Thanks Jim, looking forward to your thoughts
Comments and Questions Cancel reply
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
How to test for a positive or negative slope coefficient in regression models?
Consider the simple linear model:
$\vec Y=\beta_0+\beta_1 \vec X +\vec \varepsilon$
When I have read up on discussions about the different statistical tests that can be run on the model's slope coefficient $\beta_1$ , I have exclusively seen the following null hypothesis / alternative hypothesis set up:
\begin{align} &H_0: \beta_1 =0 \\&H_a:\beta_1 \neq 0 \end{align}
With this particular test, there is then a $t$ statistic whose formula is given as $\beta_1$ divided by the standard error of $\beta_1$ .
My question is what if I was instead interested in the following null hypothesis :
\begin{align} &H_0: \beta_1 \leq0 \\&H_a:\beta_1 \gt0 \end{align}
How exactly would I carry this out?
Is it possible to simply construct confidence intervals around $\beta_1$ (at a particular significance level) and if my resulting interval $(\beta_1-\delta,\beta_1+\delta)$ is strictly positive, I can then conclude that $\beta_1$ must be a positive number (as opposed to simply a non-zero number, which is what the prior hypothesis test would have provided us with)?
- hypothesis-testing
- 1 $\begingroup$ In Mathematical Statistics with Applications , by Wackerly, Mendenhall, and Scheaffer, Section 11.5, the authors lay out typical inferences such as $H_0: \beta_i=\beta_{i0}$ versus $H_a:\beta_i>\beta_{i0}$ or $H_a:\beta_i<\beta_{i0}$ or $H_a:\beta_i\not=\beta_{i0}.$ The test statistic is the same in all three cases, the rejection region changes. It's a fairly standard $t$ test in all three cases. Would one of these hypotheses match your research question? $\endgroup$ – Adrian Keister Commented Apr 19, 2022 at 20:29
- 1 $\begingroup$ Completely coincidentally, I just posted an answer. You can find it in the middle of stats.stackexchange.com/a/572198/919 . Look at the three short paragraphs beginning "The null hypothesis..." preceding the first figure. $\endgroup$ – whuber ♦ Commented Apr 19, 2022 at 20:29
- $\begingroup$ @whuber Thank you for the input - I read your post but am having difficulties understanding how to implement your algorithm. AdrianKeister's response has given me further pause, as well. I was always under the impression that the null hypothesis and alternative hypothesis, when unioned, had to cover the whole space of possibilities. For example, $H_0: \beta_1 \leq 0$ and $H_a: \beta_1 \gt 0$ clearly cover all cases for $\beta_1 \in \mathbb R$. However, $H_0: \beta_1 =0$ and $H_a:\beta_1 \gt 0$ do not cover all cases. Is that a problem? $\endgroup$ – S.C. Commented Apr 19, 2022 at 21:25
- $\begingroup$ First, that's not relevant to my post, because I use the first formulation. Second, it's not a problem because the test in the second case is tantamount to the test in the first case. Read about the difference between two-sided and one-sided tests for more information; but intuitively, when $\beta_1\lt 0$ it's even less likely the data will reject the hypothesis that $\beta_1=0.$ As far as implementing the algorithm goes, it amounts to halving the reported p-value and optionally subtracting it from $1:$ which part is causing difficulties in implementation? $\endgroup$ – whuber ♦ Commented Apr 19, 2022 at 22:01
Know someone who can answer? Share a link to this question via email , Twitter , or Facebook .
Your answer, sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Browse other questions tagged regression hypothesis-testing or ask your own question .
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Introducing an accessibility dashboard and some upcoming changes to display...
Hot Network Questions
- Library project - javascript
- Vilna Gaon's commentary on מחצית השקל
- What is the most economical way to fly small planes?
- Running the plot of Final Fantasy X
- Does a cancellation of an accepted review request before the due date happen often?
- What is the anti-trust argument made by X Corp's recent lawsuit against advertisers that boycotted X/Twitter
- What was the price of bottled water, and road maps, in 1995? More generally, how to find such historic prices
- Why does "take for granted" have to have the "for" in the phrase?
- What does `OP_CHECKSEPARATESIG` refer to?
- Can I say "he lived in silk" to mean he had a luxury life in which he was pampered with luxurious things?
- Groups killed by centralizing one element
- My world has a god who appears regularly to inflict punishment on wrongdoers. Is long-term sinning still possible?
- Why do many CVT cars appear to index gears during normal automatic operation?
- Can right shift operation be implemented using hardware multiplier just like left shift?
- “Ryan was like, ‘Listen, if we need cue cards…’ and I was like, ‘Cue cards? I’m showing up off-book,'” Evans recounted
- Connect electric cable with 4 wires to 3-prong 30 Amp 125-Volt/250-Volt outlet?
- Solar System Replacement?
- Why don't aircraft use D.C generators?
- Vscode how to remove Incoming/Outgoing changes graph
- Some group conditions imply non-trivial centre
- Is this really a neon lamp?
- Possible downsides of not dealing with the souls of the dead
- Can I add a PCIe card to a motherboard without rebooting, safely?
- Four Year Old Pushing and Positive Discipline Techniques
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 5, fitting a line to data.
- Estimating the line of best fit exercise
- Eyeballing the line of best fit
- Estimating with linear regression (linear models)
- Estimating equations of lines of best fit, and using them to make predictions
- Line of best fit: smoking in 1945
- Estimating slope of line of best fit
- Equations of trend lines: Phone data
Linear regression review
What is linear regression?
- (Choice A) A A A
- (Choice B) B B B
- (Choice C) C C C
- (Choice D) None of the lines fit the data. D None of the lines fit the data.
Using equations for lines of fit
Example: finding the equation.
- (Choice A) y = 5 x + 1.5 A y = 5 x + 1.5
- (Choice B) y = 1.5 x + 5 B y = 1.5 x + 5
- (Choice C) y = − 1.5 x + 5 C y = − 1.5 x + 5
- Your answer should be
- an integer, like 6
- a simplified proper fraction, like 3 / 5
- a simplified improper fraction, like 7 / 4
- a mixed number, like 1 3 / 4
- an exact decimal, like 0.75
- a multiple of pi, like 12 pi or 2 / 3 pi
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Simple Linear Regression | An Easy Introduction & Examples

Simple Linear Regression | An Easy Introduction & Examples
Published on February 19, 2020 by Rebecca Bevans . Revised on June 22, 2023.
Simple linear regression is used to estimate the relationship between two quantitative variables . You can use simple linear regression when you want to know:
- How strong the relationship is between two variables (e.g., the relationship between rainfall and soil erosion).
- The value of the dependent variable at a certain value of the independent variable (e.g., the amount of soil erosion at a certain level of rainfall).
Regression models describe the relationship between variables by fitting a line to the observed data. Linear regression models use a straight line, while logistic and nonlinear regression models use a curved line. Regression allows you to estimate how a dependent variable changes as the independent variable(s) change.
If you have more than one independent variable, use multiple linear regression instead.
Table of contents
Assumptions of simple linear regression, how to perform a simple linear regression, interpreting the results, presenting the results, can you predict values outside the range of your data, other interesting articles, frequently asked questions about simple linear regression.
Simple linear regression is a parametric test , meaning that it makes certain assumptions about the data. These assumptions are:
- Homogeneity of variance (homoscedasticity) : the size of the error in our prediction doesn’t change significantly across the values of the independent variable.
- Independence of observations : the observations in the dataset were collected using statistically valid sampling methods , and there are no hidden relationships among observations.
- Normality : The data follows a normal distribution .
Linear regression makes one additional assumption:
- The relationship between the independent and dependent variable is linear : the line of best fit through the data points is a straight line (rather than a curve or some sort of grouping factor).
If your data do not meet the assumptions of homoscedasticity or normality, you may be able to use a nonparametric test instead, such as the Spearman rank test.
If your data violate the assumption of independence of observations (e.g., if observations are repeated over time), you may be able to perform a linear mixed-effects model that accounts for the additional structure in the data.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

Simple linear regression formula
The formula for a simple linear regression is:
- y is the predicted value of the dependent variable ( y ) for any given value of the independent variable ( x ).
- B 0 is the intercept , the predicted value of y when the x is 0.
- B 1 is the regression coefficient – how much we expect y to change as x increases.
- x is the independent variable ( the variable we expect is influencing y ).
- e is the error of the estimate, or how much variation there is in our estimate of the regression coefficient.
Linear regression finds the line of best fit line through your data by searching for the regression coefficient (B 1 ) that minimizes the total error (e) of the model.
While you can perform a linear regression by hand , this is a tedious process, so most people use statistical programs to help them quickly analyze the data.
Simple linear regression in R
R is a free, powerful, and widely-used statistical program. Download the dataset to try it yourself using our income and happiness example.
Dataset for simple linear regression (.csv)
Load the income.data dataset into your R environment, and then run the following command to generate a linear model describing the relationship between income and happiness:
This code takes the data you have collected data = income.data and calculates the effect that the independent variable income has on the dependent variable happiness using the equation for the linear model: lm() .
To learn more, follow our full step-by-step guide to linear regression in R .
To view the results of the model, you can use the summary() function in R:
This function takes the most important parameters from the linear model and puts them into a table, which looks like this:

This output table first repeats the formula that was used to generate the results (‘Call’), then summarizes the model residuals (‘Residuals’), which give an idea of how well the model fits the real data.
Next is the ‘Coefficients’ table. The first row gives the estimates of the y-intercept, and the second row gives the regression coefficient of the model.
Row 1 of the table is labeled (Intercept) . This is the y-intercept of the regression equation, with a value of 0.20. You can plug this into your regression equation if you want to predict happiness values across the range of income that you have observed:
The next row in the ‘Coefficients’ table is income. This is the row that describes the estimated effect of income on reported happiness:
The Estimate column is the estimated effect , also called the regression coefficient or r 2 value. The number in the table (0.713) tells us that for every one unit increase in income (where one unit of income = 10,000) there is a corresponding 0.71-unit increase in reported happiness (where happiness is a scale of 1 to 10).
The Std. Error column displays the standard error of the estimate. This number shows how much variation there is in our estimate of the relationship between income and happiness.
The t value column displays the test statistic . Unless you specify otherwise, the test statistic used in linear regression is the t value from a two-sided t test . The larger the test statistic, the less likely it is that our results occurred by chance.
The Pr(>| t |) column shows the p value . This number tells us how likely we are to see the estimated effect of income on happiness if the null hypothesis of no effect were true.
Because the p value is so low ( p < 0.001), we can reject the null hypothesis and conclude that income has a statistically significant effect on happiness.
The last three lines of the model summary are statistics about the model as a whole. The most important thing to notice here is the p value of the model. Here it is significant ( p < 0.001), which means that this model is a good fit for the observed data.
When reporting your results, include the estimated effect (i.e. the regression coefficient), standard error of the estimate, and the p value. You should also interpret your numbers to make it clear to your readers what your regression coefficient means:
It can also be helpful to include a graph with your results. For a simple linear regression, you can simply plot the observations on the x and y axis and then include the regression line and regression function:
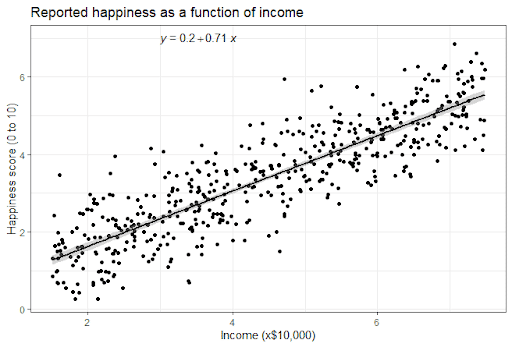
No! We often say that regression models can be used to predict the value of the dependent variable at certain values of the independent variable. However, this is only true for the range of values where we have actually measured the response.
We can use our income and happiness regression analysis as an example. Between 15,000 and 75,000, we found an r 2 of 0.73 ± 0.0193. But what if we did a second survey of people making between 75,000 and 150,000?
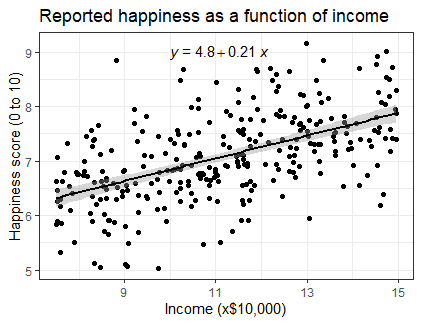
The r 2 for the relationship between income and happiness is now 0.21, or a 0.21-unit increase in reported happiness for every 10,000 increase in income. While the relationship is still statistically significant (p<0.001), the slope is much smaller than before.
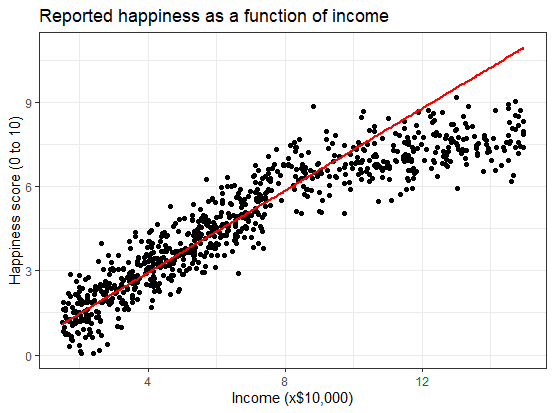
What if we hadn’t measured this group, and instead extrapolated the line from the 15–75k incomes to the 70–150k incomes?
You can see that if we simply extrapolated from the 15–75k income data, we would overestimate the happiness of people in the 75–150k income range.
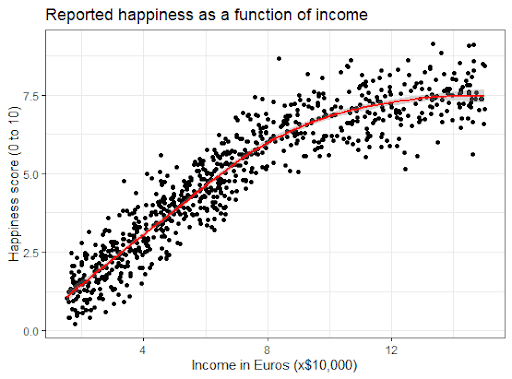
If we instead fit a curve to the data, it seems to fit the actual pattern much better.
It looks as though happiness actually levels off at higher incomes, so we can’t use the same regression line we calculated from our lower-income data to predict happiness at higher levels of income.
Even when you see a strong pattern in your data, you can’t know for certain whether that pattern continues beyond the range of values you have actually measured. Therefore, it’s important to avoid extrapolating beyond what the data actually tell you.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square test of independence
- Statistical power
- Descriptive statistics
- Degrees of freedom
- Pearson correlation
- Null hypothesis
Methodology
- Double-blind study
- Case-control study
- Research ethics
- Data collection
- Hypothesis testing
- Structured interviews
Research bias
- Hawthorne effect
- Unconscious bias
- Recall bias
- Halo effect
- Self-serving bias
- Information bias
A regression model is a statistical model that estimates the relationship between one dependent variable and one or more independent variables using a line (or a plane in the case of two or more independent variables).
A regression model can be used when the dependent variable is quantitative, except in the case of logistic regression, where the dependent variable is binary.
Simple linear regression is a regression model that estimates the relationship between one independent variable and one dependent variable using a straight line. Both variables should be quantitative.
For example, the relationship between temperature and the expansion of mercury in a thermometer can be modeled using a straight line: as temperature increases, the mercury expands. This linear relationship is so certain that we can use mercury thermometers to measure temperature.
Linear regression most often uses mean-square error (MSE) to calculate the error of the model. MSE is calculated by:
- measuring the distance of the observed y-values from the predicted y-values at each value of x;
- squaring each of these distances;
- calculating the mean of each of the squared distances.
Linear regression fits a line to the data by finding the regression coefficient that results in the smallest MSE.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Simple Linear Regression | An Easy Introduction & Examples. Scribbr. Retrieved August 5, 2024, from https://www.scribbr.com/statistics/simple-linear-regression/
Is this article helpful?
Rebecca Bevans
Other students also liked, an introduction to t tests | definitions, formula and examples, multiple linear regression | a quick guide (examples), linear regression in r | a step-by-step guide & examples, what is your plagiarism score.
Applying Classification, Regression, and Time-series Analysis
After completing this lesson, you will be able to i changed the Objective in Identify use cases where we can apply classification regression and time-series analysis techniques .
Classic Machine Learning Scenarios
This lesson covers three key Machine Learning methods for SAP HANA: Regression, Classification, and Time Series Analysis.
These methods can be utilized in various scenarios, such as:
- Regression: Effective for predicting car prices based on model characteristics and market trends.
- Classification: Useful for predicting customer behaviors, including churn, fraud detection, and purchasing patterns.
- Time Series Analysis: Ideal for forecasting future sales, demand, costs, and other metrics based on historical data.
Linear Regression: House price as a function of house‘s living area (size)
Linear regression is one of the most widely known statistical techniques. Understanding it is crucial for appreciating the development of various linear-based regression models, such as Generalized Linear Models.
Linear regression helps to uncover linear relationships, i.e., straight-line relationships, between input and output numerical variables, making it a popular technique for predictive and statistical modeling.
In the figure shown, variable "x" represents the set of values of houses' living areas, whereas variable "y" represents the prices of the houses.
The continuous values of variable "y" are predicted by "h": the function that maps the values of "x" to "y".
For simplicity, the figure only illustrates one data attribute of the houses, which is the living area. In this case, the predictor variable "x" is continuous.

Regression: Let's train a simple model from data
Similar to the previous figure, the following plot shows the input variable (houses' living areas) on the X-axis and the output variable (houses' prices) on the Y-axis.

The goal is to build a model that takes the living area of a house as input and predicts the house price. The data points in the plot represent observations from the dataset. By fitting a line to these data points, the model is created. The equation of this line is Y=mx+c, where "m" is the slope of the line and "c" is the y-intercept, i.e., the point where the line crosses the Y-axis.
Regression - Model's Performance Measurement: Mean Square Error (MSE) or L2 loss
Next, it is essential to evaluate how well the model fits the dataset, which is determined by the concept of loss. Loss measures the difference between the predicted value and the true value (ground truth).
The Mean Squared Error (MSE) or L2 loss is a loss function that computes the average of the squared differences between the predictions given by "Ŷ" and the actual sample values given by "Yi".

MSE = mean squared error
N = number of data points
Yi = observed values
Ŷi = predicted values
What is Classification?
Classification is a fundamental machine learning technique aimed at organizing input data into distinct classes. For example, the figure below illustrates how a classification model determines whether an incoming message falls under the category of SPAM or Inbox (non-SPAM).

During the classification process, the model undergoes training using the 'Training Dataset', followed by evaluation using the 'Testing Dataset'. Subsequently, the model is deployed to make predictions on new, unseen data elements.
A notable distinction between Classification and Regression tasks lies in their output variables. While Classification deals with discrete target variables, Regression tasks involve continuous output variables, as introduced in previous sections.
Time-series Analysis
Time series data is data collected about a subject at different points in time. For example, the exports of a country by year, the sales of a particular company over a period of time, or a person's blood pressure taken every minute. Any data captured continuously at different time-intervals is a type of time series data.
For example, the figure below illustrates the United Kingdom's annual mean temperatures, measured in Celsius degrees, dating back from 1800 up to recent years. The data is sourced from the Met Office or Meteorological Office Had-UK gridded dataset. The Met Office serves as the UK's national weather and climate service.

Referencing the blog of the Met Office news team (https://blog.metoffice.gov.uk/2023/07/14/how-have-daily-temperatures-shifted-in-the-uks-changing-climate/), you can discover that, utilizing 30-year meteorological averaging periods, reveals an almost 1 degree Celsius increase in the average annual mean temperature for the UK in the latest period (1991-2020) compared to the preceding period (1961-1990). This historical time-series data uncovers a long-term warming trend.
Overview of Algorithms in SAP HANA
SAP HANA has implemented a wide variety of algorithms in the categories of Classification, Regression, and Time-series analysis, and much more.
The typical algorithms for Classification are Decision Tree Analysis (CART, C4.5, CHAID), Logistic Regression, Support Vector Machine, K-Nearest Neighbor, Naïve Bayes, Confusion Matrix, AUC, Online multi-class Logistic Regression, and many more.
Whereas for Regression are Multiple Linear Regression,Online Linear Regression among others.
The most popular Time-series analysis algorithms are (Auto) Exponential Smoothing, Unified Exponential Smoothing, Linear Regression (damped trend, seas. adjust), Hierarchical Forecasting, and many more.
For details, see SAP HANA Predictive Analysis Library documentation

Log in to track your progress & complete quizzes
8.2 - Simple Linear Regression
For Bob’s simple linear regression example, he wants to see how changes in the number of critical areas (the predictor variable) impact the dollar amount for land development (the response variable). If the value of the predictor variable (number of critical areas) increases, does the response (cost) tend to increase, decrease, or stay constant? For Bob, as the number of critical features increases, does the dollar amount increase, decrease or stay the same?
We test this by using the characteristics of the linear relationships, particularly the slope as defined above. Remember from hypothesis testing, we test the null hypothesis that a value is zero. We extend this principle to the slope, with a null hypothesis that the slope is equal to zero. Non-zero slopes indicate a significant impact of the predictor variable from the response variable, whereas zero slope indicates change in the predictor variable do not impact changes in the response.
Let’s take a closer look at the linear model producing our regression results.
8.2.1 - Assumptions for the SLR Model
Before we get started in interpreting the output it is critical that we address specific assumptions for regression. Not meeting these assumptions is a flag that the results are not valid (the results cannot be interpreted with any certainty because the model may not fit the data).
In this section, we will present the assumptions needed to perform the hypothesis test for the population slope:
\(H_0\colon \ \beta_1=0\)
\(H_a\colon \ \beta_1\ne0\)
We will also demonstrate how to verify if they are satisfied. To verify the assumptions, you must run the analysis in Minitab first.
Assumptions for Simple Linear Regression
Check this assumption by examining a scatterplot of x and y.
Check this assumption by examining a scatterplot of “residuals versus fits”; the correlation should be approximately 0. In other words, there should not look like there is a relationship.
Check this assumption by examining a normal probability plot; the observations should be near the line. You can also examine a histogram of the residuals; it should be approximately normally distributed.
Check this assumption by examining the scatterplot of “residuals versus fits”; the variance of the residuals should be the same across all values of the x-axis. If the plot shows a pattern (e.g., bowtie or megaphone shape), then variances are not consistent, and this assumption has not been met.
8.2.2 - The SLR Model
The errors referred to in the assumptions are only one component of the linear model. The basis of the model, the observations are considered as coordinates, \((x_i, y_i)\), for \(i=1, …, n\). The points, \(\left(x_1,y_1\right), \dots,\left(x_n,y_n\right)\), may not fall exactly on a line, (like the cost and number of critical areas). This gap is the error!
The graph below is an example of a scatter plot showing height as the explanatory variable for height. Select the + icons to view the explanations of the different parts of the scatterplot and the least-squares regression line.
The graph below summarizes the least-squares regression for Bob's data. We will define what we mean by least squares regression in more detail later in the Lesson, for now, focus on how the red line (the regression line) "fits" the blue dots (Bob's data)
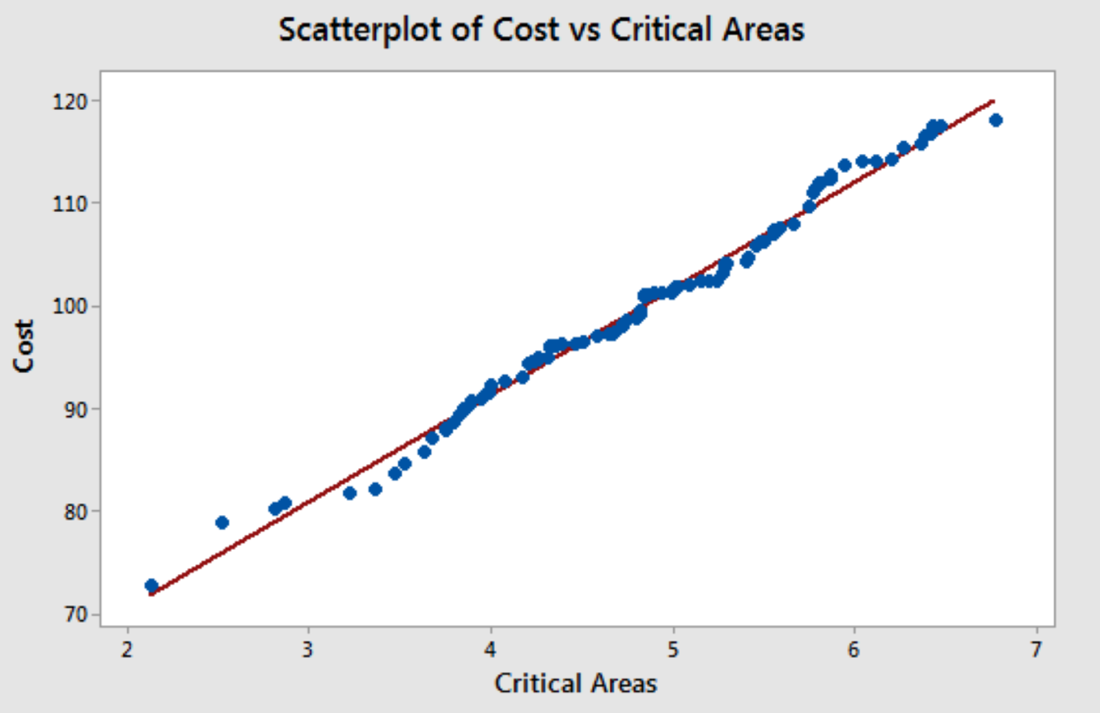
We combine the linear relationship along with the error in the simple linear regression model.
Simple Linear Regression Model
The general form of the simple linear regression model is...
\(Y=\beta_0+\beta_1X+\epsilon\)
For an individual observation,
\(y_i=\beta_0+\beta_1x_i+\epsilon_i\)
- \(\beta_0\) is the population y-intercept,
- \(\beta_1\) is the population slope, and
- \(\epsilon_i\) is the error or deviation of \(y_i\) from the line, \(\beta_0+\beta_1x_i\)
To make inferences about these unknown population parameters (namely the slope and intercept), we must find an estimate for them. There are different ways to estimate the parameters from the sample. This is where we get to n the least-squares method.
Least Squares Line
The least-squares line is the line for which the sum of squared errors of predictions for all sample points is the least.
Using the least-squares method, we can find estimates for the two parameters.
The formulas to calculate least squares estimates are:
The least squares line for Bob’s data is the red line on the scatterplot below.
Let’s jump ahead for a moment and generate the regression output. Below we will work through the content of the output. The regression output for Bob’s data look like this:
Coefficients
| Predictor | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
| Constant | 49.542 | 0.560 | 88.40 | 0.000 | |
| Critical Areas | 10.417 | 0.115 | 90.92 | 0.000 | 1.00 |
Regression Equation
Cost = 49.542 + 10.417 Critical Areas
8.2.3 - Interpreting the Coefficients
Once we have the estimates for the slope and intercept, we need to interpret them. For Bob’s data, the estimate for the slope is 10.417 and the estimate for the intercept (constant) is 49.542. Recall from the beginning of the Lesson what the slope of a line means algebraically. If the slope is denoted as \(m\), then
\(m=\dfrac{\text{change in y}}{\text{change in x}}\)
Going back to algebra, the intercept is the value of y when \(x = 0\). It has the same interpretation in statistics.
Interpreting the intercept of the regression equation, \(\hat{\beta}_0\) is the \(Y\)-intercept of the regression line. When \(X = 0\) is within the scope of observation, \(\hat{\beta}_0\) is the estimated value of Y when \(X = 0\).
Note, however, when \(X = 0\) is not within the scope of the observation, the Y-intercept is usually not of interest. In Bob’s example, \(X = 0\) or 49.542 would be a plot of land with no critical areas. This might be of interest in establishing a baseline value, but specifically, in looking at land that HAS critical areas, this might not be of much interest to Bob.
As we already noted, the slope of a line is the change in the y variable over the change in the x variable. If the change in the x variable is one, then the slope is:
\(m=\dfrac{\text{change in y}}{1}\)
The slope is interpreted as the change of y for a one unit increase in x. In Bob’s example, for every one unit change in critical areas, the cost of development increases by 10.417.
Interpreting the slope of the regression equation, \(\hat{\beta}_1\)
\(\hat{\beta}_1\) represents the estimated change in Y per unit increase in X
Note that the change may be negative which is reflected when \(\hat{\beta}_1\) is negative or positive when \(\hat{\beta}_1\) is positive.
If the slope of the line is positive, as it is in Bob’s example, then there is a positive linear relationship, i.e., as one increases, the other increases. If the slope is negative, then there is a negative linear relationship, i.e., as one increases the other variable decreases. If the slope is 0, then as one increases, the other remains constant, i.e., no predictive relationship.
Therefore, we are interested in testing the following hypotheses:
\(H_0\colon \beta_1=0\\H_a\colon \beta_1\ne0\)
Let’s take a closer look at the hypothesis test for the estimate of the slope. A similar test for the population intercept, \(\beta_0\), is not discussed in this class because it is not typically of interest.
8.2.4 - Hypothesis Test for the Population Slope
As mentioned, the test for the slope follows the logic for a one sample hypothesis test for the mean. Typically (and will be the case in this course) we test the null hypothesis that the slope is equal to zero. However, it is possible to test the null hypothesis that the slope is zero or less than zero OR test the null hypothesis that the slope is zero or greater than zero.
| Research Question | Is there a linear relationship? | Is there a positive linear relationship? | Is there a negative linear relationship? |
|---|---|---|---|
| Null Hypothesis | \(\beta_1=0\) | \(\beta_1=0\) | \(\beta_1=0\) |
| Alternative Hypothesis | \(\beta_1\ne0\) | \(\beta_1>0\) | \(\beta_1<0\) |
| Type of Test | Two-tailed, non-directional | Right-tailed, directional | Left-tailed, directional |
The test statistic for the test of population slope is:
\(t^*=\dfrac{\hat{\beta}_1}{\hat{SE}(\hat{\beta}_1)}\)
where \(\hat{SE}(\hat{\beta}_1)\) is the estimated standard error of the sample slope (found in Minitab output). Under the null hypothesis and with the assumptions shown in the previous section, \(t^*\) follows a \(t\)-distribution with \(n-2\) degrees of freedom.
Take another look at the output from Bob’s data.
Here we can see that the “T-Value” is 90.92, a very large t value indicating the difference between the null value for the slope (zero) is very different from the value for the slope calculated by the least-squares method (10.417). This results in a small probability value that the null is true (P-Value is less then .05), so Bob can reject the null, and conclude that the slope is not zero. Therefore, the number of critical areas significantly predicts the cost of development.
He can be more specific and conclude that for every one unit change in critical areas, the cost of development increases by 10.417.
As with most of our calculations, we need to allow some room for imprecision in our estimate. We return to the concept of confidence intervals to build in some error around the estimate of the slope.
The \( (1-\alpha)100\%\) confidence interval for \(\beta_1\) is:
\(\hat{\beta}_1\pm t_{\alpha/2}\left(\hat{SE}(\hat{\beta}_1)\right)\)
where \(t\) has \(n-2\) degrees of freedom.
The final piece of output from Minitab is the Least Squares Regression Equation. Remember that Bob is interested in being able to predict the development cost of land given the number of critical areas. Bob can use the equation to do this.
If a given piece of land has 10 critical areas, Bob can “plug in” the value of “10” for X, the resulting equation
\(Cost = 49.542 + 10.417 * 10\)
Results in a predicted cost of:
\(153.712 = 49.542 + 10.417 * 10\)
So, if Bob knows a piece of land has 10 critical areas, he can predict the development cost will be about 153 dollars!
Using the 10 critical features allowed Bob to predict the development cost, but there is an important distinction to make about predicting an “AVERAGE” cost, or a “SPECIFIC” cost. These are represented by ‘CONFIDENCE INTERVALS” versus ‘PREDICTION INTERVALS’ for new observations. (notice the difference here is that we are referring to a new observation as opposed to above when we used confidence intervals for the estimate of the slope!)
The mean response at a given X value is given by:
\(E(Y)=\beta_0+\beta_1X\)
Inferences about Outcome for New Observation
- The point estimate for the outcome at \(X = x\) is provided above.
- The interval to estimate the mean response is called the confidence interval. Minitab calculates this for us.
- The interval used to estimate (or predict) an outcome is called prediction interval.
For a given x value, the prediction interval and confidence interval have the same center, but the width of the prediction interval is wider than the width of the confidence interval. That makes good sense since it is harder to estimate a value for a single subject (for example a particular piece of land in Bob’s town that may have some unique features) than it would be to estimate the average for all pieces of land. Again, Minitab will calculate this interval as well.
8.2.5 - SLR with Minitab
Minitab ®, simple linear regression with minitab.
- Select Stat > Regression > Regression > Fit Regression Model
- In the box labeled " Response ", specify the desired response variable.
- In the box labeled " Predictors ", specify the desired predictor variable.
- Select OK . The basic regression analysis output will be displayed in the session window.
To check assumptions...
- Click Graphs .
- In 'Residuals plots, choose 'Four in one.'
- Select OK .

IMAGES
VIDEO
COMMENTS
The formula for the t-test statistic is t = b1 √(MSE SSxx) Use the t-distribution with degrees of freedom equal to n − p − 1. The t-test for slope has the same hypotheses as the F-test: Use a t-test to see if there is a significant relationship between hours studied and grade on the exam, use α = 0.05.
Hypothesis Test for Regression Slope. This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y.. The test focuses on the slope of the regression line Y = Β 0 + Β 1 X. where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of ...
For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are: Hypothesis test for testing that all of the slope parameters are 0. Hypothesis test for testing ...
Conducting a Hypothesis Test for a Regression Slope. To conduct a hypothesis test for a regression slope, we follow the standard five steps for any hypothesis test: Step 1. State the hypotheses. The null hypothesis (H0): B 1 = 0. The alternative hypothesis: (Ha): B 1 ≠ 0. Step 2. Determine a significance level to use.
xi: The value of the predictor variable xi. Multiple linear regression uses the following null and alternative hypotheses: H0: β1 = β2 = … = βk = 0. HA: β1 = β2 = … = βk ≠ 0. The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically ...
c plot.9.2 Statistical hypothesesFor simple linear regression, the chief null hypothesis is H0 : β1 = 0, and the corresponding alter. ative hypothesis is H1 : β1 6= 0. If this null hypothesis is true, then, from E(Y ) = β0 + β1x we can see that the population mean of Y is β0 for every x value, which t.
In Chapter 6, the relationship between Hematocrit and body fat % for females appeared to be a weak negative linear association. The 95% confidence interval for the slope is -0.186 to 0.0155. For a 1% increase in body fat %, we are 95% confident that the change in the true mean Hematocrit is between -0.186 and 0.0155% of blood.
In this Lesson, we will first introduce the Simple Linear Regression (SLR) Model and the Correlation Coefficient. ... Some of you may have noticed that the hypothesis test for correlation and slope are very similar. Also, the test statistic for both tests follows the same distribution with the same degrees of freedom, \(n-2\).
And for this situation where our alternative hypothesis is that our true population regression slope is greater than zero, our P-value can be viewed as the probability of getting a T-statistic greater than or equal to this. So getting a T-statistic greater than or equal to 2.999.
Therefore, the confidence interval is b2 +/- t × SE (b). *b) Hypothesis Testing:*. The null hypothesis is that the slope of the population regression line is 0. that is Ho : B =0. So, anything other than that will be the alternate hypothesis and thus, Ha : B≠0. This is the stuff covered in the video and I hope it helps!
Objectives. Upon completion of this lesson, you should be able to: Distinguish between a deterministic relationship and a statistical relationship. Understand the concept of the least squares criterion. Interpret the intercept b 0 and slope b 1 of an estimated regression equation. Know how to obtain the estimates b 0 and b 1 from Minitab's ...
Whenever we perform linear regression, we want to know if there is a statistically significant relationship between the predictor variable and the response variable. We test for significance by performing a t-test for the regression slope. We use the following null and alternative hypothesis for this t-test: H 0: β 1 = 0 (the slope is equal to ...
Equation for a Line. Think back to algebra and the equation for a line: y = mx + b. In the equation for a line, Y = the vertical value. M = slope (rise/run). X = the horizontal value. B = the value of Y when X = 0 (i.e., y-intercept). So, if the slope is 3, then as X increases by 1, Y increases by 1 X 3 = 3. Conversely, if the slope is -3, then ...
So our null hypothesis here would be that the true slope of the true regression line, this, the parameter right over here, is equal to zero. So beta is equal to zero. So our null hypothesis actually might be that our true regression line might look something like this. That what y is, is somewhat independent of what x is.
We now show how to test the value of the slope of the regression line. Basic Approach. By Property 1 of One Sample Hypothesis Testing for Correlation, under certain conditions, the test statistic t has the property. But by Property 1 of Method of Least Squares. and by Definition 3 of Regression Analysis and Property 4 of Regression Analysis. Putting these elements together we get that
In simple linear regression, this is equivalent to saying "Are X an Y correlated?". In reviewing the model, Y = β0 +β1X + ε Y = β 0 + β 1 X + ε, as long as the slope ( β1 β 1) has any non‐zero value, X X will add value in helping predict the expected value of Y Y. However, if there is no correlation between X and Y, the value of ...
An \(\alpha\)-level hypothesis test for the slope parameter \(\beta_{1}\) Section . We follow standard hypothesis test procedures in conducting a hypothesis test for the slope \(\beta_{1}\). ... In rare circumstances, it may make sense to consider a simple linear regression model in which the intercept, \(\beta_{0}\), is assumed to be exactly 0 ...
Consider the simple linear model: $\vec Y=\beta_0+\beta_1 \vec X +\vec \varepsilon$ When I have read up on discussions about the different statistical tests that can be run on the model's slope coefficient $\beta_1$, I have exclusively seen the following null hypothesis / alternative hypothesis set up:
Write a linear equation to describe the given model. Step 1: Find the slope. This line goes through ( 0, 40) and ( 10, 35) , so the slope is 35 − 40 10 − 0 = − 1 2 . Step 2: Find the y -intercept. We can see that the line passes through ( 0, 40) , so the y -intercept is 40 . Step 3: Write the equation in y = m x + b form.
In simple linear regression, p=1, and the coefficient is known as regression slope. Statistical estimation and inference in linear regression focuses on β. The elements of this parameter vector are interpreted as the partial derivatives of the dependent variable with respect to the various independent variables.
Regression allows you to estimate how a dependent variable changes as the independent variable (s) change. Simple linear regression example. You are a social researcher interested in the relationship between income and happiness. You survey 500 people whose incomes range from 15k to 75k and ask them to rank their happiness on a scale from 1 to ...
Linear regression is one of the most widely known statistical techniques. Understanding it is crucial for appreciating the development of various linear-based regression models, such as Generalized Linear Models. ... The equation of this line is Y=mx+c, where "m" is the slope of the line and "c" is the y-intercept, i.e., the point where the ...
For Bob's simple linear regression example, he wants to see how changes in the number of critical areas (the predictor variable) impact the dollar amount for land development (the response variable). ... We extend this principle to the slope, with a null hypothesis that the slope is equal to zero. Non-zero slopes indicate a significant impact ...
In simple linear regression, this is equivalent to saying "Are X an Y correlated?". In reviewing the model, Y = β0 +β1X + ε Y = β 0 + β 1 X + ε, as long as the slope ( β1 β 1) has any non‐zero value, X X will add value in helping predict the expected value of Y Y. However, if there is no correlation between X and Y, the value of ...
2+ years of experience working with linear regression, logistic regression, random forest, gradient boosting algorithms and other similar machine learning ... AB testing, hypothesis testing, linear and logistic regression). How you'll make an impact. Posted Posted 30+ days ago ...