Binomial Distribution Calculator
What is the binomial probability, binomial probability formula, how to use the binomial distribution calculator: an example, how to calculate cumulative probabilities, binomial probability distribution experiments, mean and variance of binomial distribution, other considerations.
This binomial distribution calculator is here to help you with probability problems in the following form: what is the probability of a certain number of successes in a sequence of events? Read on to learn what exactly is the binomial probability distribution, when and how to apply it, and learn the binomial probability formula. Find out what is binomial distribution, and discover how binomial experiments are used in various settings.
Imagine you're playing a game of dice. To win, you need exactly three out of five dice to show a result equal to or lower than 4. The remaining two dice need to show a higher number. What is the probability of you winning?
This is a sample problem that can be solved with our binomial probability calculator. You know the number of events (it is equal to the total number of dice, so five); you know the number of successes you need (precisely 3); you also can calculate the probability of one single success occurring (4 out of 6, so 0.667). This is all the data required to find the binomial probability of you winning the game of dice.
Note that to use the binomial distribution calculator effectively, the events you analyze must be independent . It means that all the trials in your example are supposed to be mutually exclusive.
The first trial's success doesn't affect the probability of success or the probability of failure in subsequent events, and they stay precisely the same. In the case of a dice game, these conditions are met: each time you roll a die constitutes an independent event.
Sometimes you may be interested in the number of trials you need to achieve a particular outcome. For instance, you may wonder how many rolls of a die are necessary before you throw a six three times. Such questions may be addressed using a related statistical tool called the negative binomial distribution. Make sure to learn about it with Omni's negative binomial distribution calculator .
Also, you may check our normal approximation to binomial distribution calculator and the related continuity correction calculator.
To find this probability, you need to use the following equation:
P(X=r) = nCr × p r × (1-p) n-r
- n – Total number of events;
- r – Number of required successes;
- p – Probability of one success;
- nCr – Number of combinations (so-called "n choose r"); and
- P(X=r) – Probability of an exact number of successes happening.
You should note that the result is the probability of an exact number of successes. For example, in our game of dice, we needed precisely three successes – no less, no more. What would happen if we changed the rules so that you need at least three successes? Well, you would have to calculate the probability of exactly three, precisely four, and precisely five successes and sum all of these values together.
Let's solve the problem of the game of dice together.
Determine the number of events. n is equal to 5, as we roll five dice.
Determine the required number of successes. r is equal to 3, as we need exactly three successes to win the game.
The probability of rolling 1, 2, 3, or 4 on a six-sided die is 4 out of 6, or 0.667. Therefore p is equal to 0.667 or 66.7%.
Calculate the number of combinations (5 choose 3). You can use the combination calculator to do it. This number, in our case, is equal to 10.
Substitute all these values into the binomial probability formula above:
P(X = 3) = 10 × 0.667 3 × (1-0.667) (5-3) = 10 × 0.667 3 × (1-0.667) (5-3) = 10 × 0.296 × 0.333 2 = 2.96 × 0.111 = 0.329
You can also save yourself some time and use the binomial distribution calculator instead :)
Sometimes, instead of an exact number of successes, you want to know the probability of getting r or more successes or r or less successes. To calculate the probability of getting any range of successes:
- Use the binomial probability formula to calculate the probability of success (P) for all possible values of r you are interested in.
- Sum the values of P for all r within the range of interest.
For example, the probability of getting two or fewer successes when flipping a coin four times (p = 0.5 and n = 4) would be:
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
P(X ≤ 2) = 37.5% + 25% + 6.25%
P(X ≤ 2) = 68.75%
This calculation is made easy using the options available on the binomial distribution calculator. You can change the settings to calculate the probability of getting:
- Exactly r successes: P(X = r)
- r or more successes: P(X ≥ r)
- r or fewer successes: P(X ≤ r)
- Between r₀ and r₁ successes P(r₀ ≤ X ≤ r₁)
The binomial distribution turns out to be very practical in experimental settings . However, the output of such a random experiment needs to be binary : pass or failure, present or absent, compliance or refusal. It's impossible to use this design when there are three possible outcomes.
At the same time, apart from rolling dice or tossing a coin, it may be employed in somehow less clear cases. Here are a couple of questions you can answer with the binomial probability distribution:
- Will a new drug work on a randomly selected patient?
- Will a light bulb you just bought work properly, or will it be broken?
- What is a chance of correctly answering a test question you just drew?
- What is a probability of a random voter to vote for a candidate in an election?
- How likely is it for a group of students to be accepted to a prestigious college?
Experiments with precisely two possible outcomes, such as the ones above, are typical binomial distribution examples, often called the Bernoulli trials .
In practice, you can often find the binomial probability examples in fields like quality control , where this method is used to test the efficiency of production processes. The inspection process based on the binomial distribution is designed to perform a sufficient number of checkups and minimize the chances of manufacturing a defective product.
If you don't know the probability of an independent event in your experiment ( p ), collect the past data in one of your binomial distribution examples, and divide the number of successes ( y ) by the overall number of events p = y/n .
Once you have determined your rate of success (or failure) in a single event, you need to decide what's your acceptable number of successes (or failures) in the long run. For example, one defective product in a batch of fifty is not a tragedy, but you wouldn't like to have every second product faulty, would you?
Bernoulli trials are also perfect at solving network systems . Interestingly, they may be used to work out paths between two nodes on a diagram. This is the case of the Wheatstone bridge network, a representation of a circuit built for electrical resistance measurement.
Like the binomial distribution table , our calculator produces results that help you assess the chances that you will meet your target. However, if you like, you may take a look at this binomial distribution table . It tells you what is the binomial distribution value for a given probability and number of successes.
One of the most exciting features of binomial distributions is that they represent the sum of a number n of independent events. Each of them ( Z ) may assume the values of 0 or 1 over a given period.
Let's say the probability that each Z occurs is p . Since the events are not correlated, we can use random variables' addition properties to calculate the mean (expected value) of the binomial distribution μ = np .
The variance of a binomial distribution is given as: σ² = np(1-p) . The larger the variance, the greater the fluctuation of a random variable from its mean. A small variance indicates that the results we get are spread out over a narrower range of values.
The standard deviation of binomial distribution, another measure of a probability distribution dispersion, is simply the square root of the variance, σ . Keep in mind that the standard deviation calculated from your sample (the observations you actually gather) may differ from the entire population's standard deviation. If you find this distinction confusing, there here's a great explanation of this distinction .
There's a clear-cut intuition behind these formulas. Suppose this time that I flip a coin 20 times:
- My p is then equal to 0.5 (unless, of course, the coin is rigged);
- Each Z has an equivalent chance of 0 or 1;
- The number of trials, n , is 20.
This sequence of events fulfills the prerequisites of a binomial distribution.
The mean value of this simple experiment is: np = 20 × 0.5 = 10 . We can say that on average if we repeat the experiment many times, we should expect heads to appear ten times.
The variance of this binomial distribution is equal to np(1-p) = 20 × 0.5 × (1-0.5) = 5 . Take the square root of the variance, and you get the standard deviation of the binomial distribution, 2.24 . Accordingly, the typical results of such an experiment will deviate from its mean value by around 2. Hence, in most of the trials, we expect to get anywhere from 8 to 12 successes.
Use our binomial probability calculator to get the mean, variance, and standard deviation of binomial distribution based on the number of events you provided and the probability of one success.
Developed by a Swiss mathematician Jacob Bernoulli , the binomial distribution is a more general formulation of the Poisson distribution. In the latter, we simply assume that the number of events (trials) is enormous, but the probability of a single success is small.
The binomial distribution is closely related to the binomial theorem , which proves to be useful for computing permutations and combinations. Make sure to check out our permutations calculator , too!
Keep in mind that the binomial distribution formula describes a discrete distribution . The possible outcomes of all the trials must be distinct and non-overlapping. What's more, the two outcomes of an event must be complementary: for a given p , there's always an event of q = 1-p .
If there's a chance of getting a result between the two, such as 0.5, the binomial distribution formula should not be used. The same goes for the outcomes that are non-binary, e.g., an effect in your experiment may be classified as low, moderate, or high.
However, for a sufficiently large number of trials, the binomial distribution formula may be approximated by the Gaussian (normal) distribution specification, with a given mean and variance. That allows us to perform the so-called continuity correction , and account for non-integer arguments in the probability function.
Maybe you still need some practice with the binomial probability distribution examples?
Try to solve the dice game's problem again, but this time you need three or more successes to win it. How about the chances of getting exactly 4?

Is the binomial distribution discrete or continuous?
The binomial distribution is discrete – it takes only a finite number of values.
How do I find the mean of a binomial distribution?
To calculate the mean (expected value) of a binomial distribution B(n,p) you need to multiply the number of trials n by the probability of successes p , that is: mean = n × p .
How do I find the standard deviation of a binomial distribution?
To find the standard deviation of a binomial distribution B(n,p) :
- Compute the variance as n × p × (1-p) , where n is the number of trials and p is the probability of successes.
- Take the square root of the number obtained in Step 1.
- That's it! Congrats :)
What is the probability of 3 successes in 5 trials if the probability of success is 0.5?
To find this probability, you need to:
Recall the binomial distribution formula P(X = r) = nCr × pʳ × (1-p)ⁿ⁻ʳ . We'll use it with the following data:
Number of trials: n = 5 ;
Number of successes: r = 3 ; and
Probability of success: p = 0.5 .
Calculate 5 choose 3 : nCr = 10 .
Plug these values into the formula:
P(X = 3) = 10 × 0.5² × 0.5³ = 0.3125 .
The probability you're looking for is 31.25% .
Car crash force
Lognormal distribution, random dice roller.
- Biology (103)
- Chemistry (101)
- Construction (148)
- Conversion (304)
- Ecology (32)
- Everyday life (263)
- Finance (597)
- Health (443)
- Physics (513)
- Sports (108)
- Statistics (184)
- Other (186)
- Discover Omni (40)

Best Online Statistics Calculators and Tutorials
Binomial probability calculator.
Trials (n): *
Probability (p): *
Successes (X): *
Type of probability: * Exactly X successes Less than X successes At most X successes More than X successes At least X successes
$ P(1) $ Probability of exactly 1 successes: 0.0487703125
$P(1)$ Probability of exactly 1 successes
If using a calculator, you can enter $ \text{trials} = 5 $, $ p = 0.65 $, and $ X = 1 $ into a binomial probability distribution function (PDF). If doing this by hand, apply the binomial probability formula: $$ P(X) = \binom{n}{X} \cdot p^X \cdot (1-p)^{n-X} $$ The binomial coefficient, $ \binom{n}{X} $ is defined by $$ \binom{n}{X} = \frac{n!}{X!(n-X)!} $$ The full binomial probability formula with the binomial coefficient is $$ P(X) = \frac{n!}{X!(n-X)!} \cdot p^X \cdot (1-p)^{n-X} $$ where $n$ is the number of trials, $p$ is the probability of success on a single trial, and $X$ is the number of successes. Substituting in values for this problem, $ n = 5 $, $ p = 0.65 $, and $ X = 1 $. $$ P(1) = \frac{5!}{1!(5-1)!} \cdot 0.65^1 \cdot (1-0.65)^{5-1} $$ Evaluating the expression, we have $$ P(1) = 0.0487703125 $$
Complete Binomial Distribution Table
If we apply the binomial probability formula, or a calculator's binomial probability distribution (PDF) function, to all possible values of X for 5 trials, we can construct a complete binomial distribution table. The sum of the probabilities in this table will always be 1. The complete binomial distribution table for this problem, with p = 0.65 and 5 trials is:
P(0) = 0.0052521875 P(1) = 0.0487703125 P(2) = 0.181146875 P(3) = 0.336415625 P(4) = 0.3123859375 P(5) = 0.1160290625
Binomial Probability Calculator
- Binomial Probability
As we continue our journey through the intricate world of statistics, we encounter a fundamental concept: binomial probability. This foundational idea is a cornerstone of various scientific, economic, and social disciplines, applicable everywhere. Our goal is to help you grasp this concept effectively, and to assist in that endeavor, we present our Binomial Probability Calculator - a user-friendly tool designed to make your calculations as straightforward as possible.
Delving Deeper into Binomial Probability
At its core, binomial probability deals with discrete events happening in a fixed number of independent trials, each having two possible outcomes - success or failure. The classic example of a binomial experiment is flipping a coin - with only two outcomes (heads or tails), and each flip independent from the next.
The mathematical formula that represents binomial probability is as follows:
P(x; n, p) = \binom{n}{x} \cdot p^{x} \cdot (1 - p)^{n-x}
This formula breaks down into:
- P(x; n, p): the probability of x successes in n trials
- C(n, x): the combination function, representing the number of possible combinations of n trials taken x at a time
- p: the probability of success on a single trial
- (1 - p): the probability of failure (often represented as q)
This formula allows us to calculate the probability of obtaining a specific number of successes in a set number of trials.
Unleashing the Potential of the Binomial Probability Calculator
Our calculator is designed to save you the hassle of performing complex calculations manually. It offers a user-friendly interface, allowing you to input your values and receive an accurate, instant result. This precision and speed free up your time and cognitive resources, enabling you to focus on interpreting the results and applying them in your context.
Guidance on Using the Binomial Probability Calculator
The operation of our calculator is simple. Follow these steps to get your result:
- Enter Your Values: You will input three parameters: the number of trials (n), the number of successful outcomes you are calculating the probability for (x), and the probability of success on a single trial (p).
- Review Your Result: The binomial probability will be displayed instantly.
Walking Through an Example: The Binomial Probability Calculator in Action
To demonstrate the utility of our calculator, let's consider a classic example.
Imagine flipping a fair coin (where the probability of landing on heads, p, equals 0.5) ten times. You want to know the probability of getting exactly five heads.
Let's run these values through our calculator:
- Input Values: Enter 10 for the number of trials (n), 5 for the number of successful outcomes (x), and 0.5 for the probability of success (p).
- Review: The calculator promptly computes the binomial probability, providing the likelihood of getting exactly 5 heads in 10 flips.
The Versatility and Applicability of Binomial Probability
Binomial probability finds applications across various domains:
- Finance: Investors often use binomial probability to understand the likelihood of a specific number of investments being successful.
- Quality Control: Manufacturers can use it to predict the number of defective items in a large batch.
- Biology: Geneticists use binomial probability to calculate the chances of organisms inheriting specific traits.
- Sports: Coaches and analysts use it to analyze patterns of win and loss, making strategic decisions based on the results.
- Survey and Poll Analysis: It can help interpret the results of yes/no questions across a sample population.
Our Binomial Probability Calculator is your go-to tool for all these applications and more. Whether you're a student trying to complete your statistics homework, a researcher examining the effects of a new drug, or a market analyst trying to predict future trends, our calculator can facilitate your work and boost your understanding of binomial probability.
Always remember, statistics is not just about number crunching. It's about making sense of patterns, understanding uncertainty, and making informed decisions based on the data at hand. Our Binomial Probability Calculator is a stepping stone on your journey to statistical mastery. Enjoy exploring and happy calculating!
- Probability and Discrete Distributions
- Continuous Distributions and Data Visualization
- Conditional Probability
- Bayes Theorem
- Expected Value
- Poisson Probability
- Geometric Probability
- Hypergeometric Probability
- Birthday Paradox
- Chebyshev's Theorem
- Coin Flip Probability
- Coin Toss Streak
- Implied Probability
- Post-Test Probability
- Random Number
- Relative Risk
- Normal Distribution
- Chi-Square Distribution
- F-Distribution
- Exponential Distribution
- Benford's Law
- Central Limit Theorem (CLT)
Binomial Distribution Calculator
Statscalculator.com, related tools.
Probability (p)
# Trials (n)
# Success (X)
How to Use a Binomial Probability Calculator: Mastering Distributions and Outcomes
The world of probability and statistics can be complex, but with the right tools, even the most challenging probabilities become easier to understand. One such tool is the binomial probability calculator, specifically designed to handle problems involving binomial distribution. This powerful calculator makes it simple to compute binomial probability, variance, standard deviation, and other related measures with a few clicks, streamlining the process and providing accurate results.
A binomial experiment is a discrete probability distribution that consists of a fixed number of trials, each with two possible outcomes: success and failure. The probability of success (p) is constant across each trial, and the trials are independent of one another. The binomial distribution calculator utilizes the binomial probability formula to compute the probability mass function, calculating the probability of obtaining k successes in n trials. It can also compute the cumulative distribution function, providing probabilities for cumulative events, such as the probability that a fair coin will land heads at least three times in five tosses.
In addition to calculating probabilities, the binomial probability calculator can also compute standard deviation, variance, and expected value for a binomial random variable. These calculations are crucial in determining the shape and spread of a distribution curve, as well as the likelihood of specific outcomes. With this comprehensive tool, both students and professionals can confidently approach questions and problems involving binomial distribution and gain a deeper understanding of discrete probability distribution and related concepts.
Using a Binomial Probability Calculator
Calculator features.
A binomial probability calculator is a useful tool for calculating probabilities based on the binomial distribution. This calculator can determine the probability of a specific number of successes occurring in a fixed number of trials, given the probability of success in each trial. It provides various types of probabilities, including equal to, less than, more than, at most, and at least the target number of successes.
In addition to probability calculations, the binomial probability calculator can also generate the mean, variance, and standard deviation of the binomial distribution. These statistics provide insights into the expected value, spread, and deviation of the distribution, allowing for a comprehensive understanding of the binomial experiment.
Input Values
To use a binomial probability calculator, you need to input the following values:
- Probability of success (p): The probability of a successful outcome in a single trial.
- Number of trials (n): The total number of trials conducted in the binomial experiment.
- Target number of successes (k): The specific number of successful outcomes you are interested in.
Once the required input values are entered, the calculator will generate the probabilities for different events, such as:
| Event Type | Probability |
|---|---|
| Equal to k successes | P(X=k) |
| Less than k successes | P(X<k) |
| More than k successes | P(X>k) |
| At most k successes | P(X≤k) |
| At least k successes | P(X≥k) |
These results can be useful for understanding the likelihood of various outcomes in a binomial experiment, such as the probability of flipping a fair coin a certain number of times and obtaining a specific number of heads. The binomial probability calculator also computes the mean, variance, and standard deviation of the binomial distribution, providing a deeper understanding of the experiment's statistical properties.
Using a binomial probability calculator is an efficient way to analyze binomial experiments and gain insights into the probabilities of different events occurring. With a clear, neutral, and knowledgeable tone, this tool can help you make informed decisions based on statistical evidence, enhancing your understanding of discrete probability distributions and their applications in real-world scenarios.
Understanding Binomial Probability
Binomial experiment.
A binomial experiment is a statistical experiment consisting of a fixed number of trials, each with two possible outcomes, success or failure. Each trial is independent, and the probability of success and failure remains constant throughout the experiment. Examples of binomial experiments include flipping a fair coin or rolling a die.
Success and Failure
In a binomial experiment, the two outcomes are termed success and failure. The probability of success, denoted as p, is the chance of a successful outcome occurring, while the probability of failure, denoted as (1-p), is the chance of an unsuccessful outcome occurring. For example, in a fair coin flip, the probability of success (getting heads) is 0.5, while the probability of failure (getting tails) is also 0.5.
Independent Events
Events are said to be independent when the occurrence of one event does not affect the occurrence of the other event. In a binomial experiment, trials are independent, meaning that the outcome of one trial has no impact on the outcomes of subsequent trials. This is an important aspect when using a binomial probability calculator.
A binomial probability distribution represents the probabilities of obtaining k successes in n trials, with each trial having only two possible outcomes. The binomial probability formula is as follows:
P(X = k) = (C(n, k) * p^k * (1-p)^(n-k))
- P(X = k) is the probability of obtaining k successes
- n is the number of trials
- k is the number of successful outcomes
- p is the probability of success in each trial
- C(n, k) is the binomial coefficient, or the number of k-combinations for n elements
To use a binomial probability calculator , follow these steps:
- Enter the number of trials, n.
- Enter the probability of success, p.
- Enter the number of successful outcomes, k.
The calculator will then output the probability of obtaining k successes in n trials based on the given values for success and failure.
The binomial distribution has many properties, including mean, variance, and standard deviation, which help describe its shape and location on the distribution curve. The expected value (mean) of a binomial distribution is given by E(X) = np, and the variance is given by V(X) = np(1-p). The standard deviation is the square root of the variance.
In summary, understanding binomial probability involves grasping the concepts of binomial experiments, success and failure, independent events, and the probability distribution. A binomial probability calculator can be a useful tool for calculating the probabilities of various outcomes in binomial experiments, enabling us to make informed decisions in real-world applications of statistics.
Binomial Distribution Basics
Probability distribution.
The binomial distribution is a discrete probability distribution used to model the probability of obtaining k successes in n trials of a binomial experiment. A binomial experiment has the following characteristics:
- Each trial has only two possible outcomes: success or failure.
- The probability of success p remains constant across all trials.
- The trials are independent of each other.
The binomial probability formula calculates the probability of obtaining exactly k successes in n trials, given as: P(X = k) = C(n, k) * p^k * (1-p)^(n-k)
where C(n, k) is the binomial coefficient, p is the probability of success, and (1-p) is the probability of failure.
The mean, or expected value, of a binomial distribution is the expected number of successes in the n trials, given as: μ = n * p
The variance is a measure of how far the outcomes of the binomial experiment are from the mean. The variance in a binomial distribution is given as: σ^2 = n * p * (1-p)
Standard Deviation
The standard deviation in a binomial distribution is the square root of the variance, measuring the average distance of individual outcomes from the mean. It is given as: σ = √(n * p * (1-p))
A binomial probability calculator can compute the binomial distribution, probabilities, mean, variance, and standard deviation by inputting the number of trials, success probability, and the desired number of successes. This tool helps answer questions related to binomial experiments, such as probability distributions, cumulative probabilities, and distribution curves.
Calculating Binomial Probabilities
In this section, we discuss how to use a binomial probability calculator to determine the probability of various outcomes in a binomial experiment.
Binomial Probability Formula
The binomial probability formula gives the probability of observing k successes in n trials, where each trial has a probability of success p. The formula is as follows:
P(X=k) = C(n, k) * p^k * (1-p)^(n-k)
- P(X=k) is the probability of k successes
- C(n, k) is the number of possible combinations of n trials and k successes
- p is the probability of success for each trial
Combinations
To calculate the number of combinations, C(n, k), we use the binomial coefficient formula:
C(n, k) = n! / (k! * (n-k)!)
- n! is the factorial of n, which is the product of all positive integers up to n
- k! is the factorial of k
- (n-k)! is the factorial of (n-k)
Using a binomial probability calculator, you can input the desired values for n, k, and p to compute the probability of achieving k successes in n trials.
To illustrate this process, let's consider a simple experiment: tossing a fair coin. The probability of success (obtaining a head) in each trial (toss) is 0.5. We can calculate the binomial probability for obtaining a certain number of heads in a defined number of tosses.
For example, if we want to calculate the probability of obtaining exactly 5 heads in 10 coin tosses, we input the following values:
- n = 10 (number of trials)
- k = 5 (number of successful outcomes)
- p = 0.5 (probability of success for each trial)
Using the binomial probability formula and calculator, we can determine the probability of obtaining exactly 5 heads in 10 coin tosses.
It's essential to understand that the binomial probability distribution is a discrete probability distribution, meaning that it consists of distinct, non-overlapping outcomes. This is in contrast to continuous distributions, which have a continuous range of possible outcomes.
By calculating binomial probabilities, one can gain insights into various real-life scenarios, such as predicting the number of successful outcomes in a certain experiment or event, and find the expected value and standard deviation of a binomial random variable. This information is invaluable in fields like statistics and data analytics, where understanding the chance of success and possible outcomes is critical for decision-making.
Types of Binomial Probability Questions
In this section, we will discuss two main types of binomial probability questions: Cumulative Probabilities and Specific Scenarios.
Cumulative Probabilities
Cumulative probabilities refer to the probability of getting a certain number of successes or a range of successful outcomes in a binomial experiment. Some common types of cumulative probability questions include:
- Exactly k successes: This calculates the probability of getting exactly k successes in n trials.
- At least k successes: This determines the probability of getting k or more successes in n trials.
- At most k successes: This computes the probability of getting k or fewer successes in n trials.
- More than k successes: This finds the probability of getting more than k successes in n trials.
- Less than k successes: This calculates the probability of getting less than k successes in n trials.
To calculate cumulative probabilities, one can use the binomial probability mass function (PMF) in combination with the binomial coefficient. Additionally, the cumulative distribution function (CDF) can be utilized.
Specific Scenarios
Specific Scenarios refer to more focused binomial probability questions that deal with individual events or unique situations. Examples include:
- Fair coin toss : If a fair coin is flipped n times, what is the probability of getting k heads (successes) and (n-k) tails (failures)?
- Probability of defective items : In a manufacturing process, a certain percentage of items are defective. What is the probability of finding exactly k defective items in a sample of size n?
To calculate binomial probabilities in specific scenarios, one can use the binomial probability formula or the binomial distribution calculator. The calculator can typically handle all the types of questions discussed in the Cumulative Probabilities subsection.
Remember, when working with binomial probability questions, the following elements are essential:
- Number of trials (n)
- Probability of success (p)
- Number of successful outcomes (k)
Understanding the types of binomial probability questions and their corresponding methods of calculation can help better analyze real-world scenarios and make data-driven decisions.
Comparing Distributions
Normal distribution.
The normal distribution is a continuous probability distribution that is symmetrical and bell-shaped. It is often used in statistics to model natural occurrences and is seen as a general representation for the distribution of real-life events.
- Probability distribution: Continuous
- Parameters: Mean (μ), Standard deviation (σ)
- Characteristics: Symmetrical, bell-shaped
A continuous distribution, like the normal distribution, maps the probabilities of continuous events, which have infinitely many possible outcomes. Although it is different from the discrete probability distributions such as the binomial distribution, it's useful to compare their main characteristics.
Negative Binomial Distribution
The negative binomial distribution, on the other hand, is a discrete probability distribution that models the number of successes in a fixed number of Bernoulli trials (independent experiments with binary outcomes) before a specified number of failures occur.
- Probability distribution: Discrete
- Parameters: Number of successful outcomes (k), probability of success (p)
- Characteristics: Skewed, dependent on the target number of failures
The negative binomial distribution is related to the binomial distribution, as both are discrete distributions that describe the probabilities associated with a binomial experiment. However, the negative binomial distribution focuses on the number of trials needed to reach a certain number of failures, rather than specifying a fixed number of trials (n trials) as in the binomial distribution.
| Distribution Type | Probability distribution | Parameters | Shape |
|---|---|---|---|
| Normal Distribution | Continuous | Mean (μ), Standard deviation (σ) | Symmetrical, bell-shaped |
| Negative Binomial Distribution | Discrete | Number of successful outcomes (k), probability of success (p) | Skewed, dependent on the target number of failures |
These comparisons help in understanding the differences between the normal distribution, negative binomial distribution, and the binomial distribution. When solving statistical problems and answering questions, choosing the appropriate distribution is crucial for accurate calculations and interpretations.
Real-Life Applications
Coin tosses.
A binomial probability calculator is highly useful in calculating probabilities related to coin tosses. Coin tosses represent a classic example of a binomial experiment, where there are two possible outcomes: success (head) and failure (tail). In this scenario, the success probability p remains constant at 0.5, as we assume a fair coin.
When dealing with coin tosses, we often deal with the binomial probability distribution, which is a discrete probability distribution. The binomial probability mass function, which represents the probability of k successes in n trials, is given by the binomial probability formula:
Where C(n, k) = n! / [k!(n-k)!] (the binomial coefficient) and p represents the probability of success.
Using a binomial distribution calculator, one can find the probability of a specific number of successes, as well as cumulative probabilities and expected values. This is essential in answering questions related to coin tosses and statistical analysis.
Another real-life application for the binomial probability calculator is dice rolls. A standard six-sided die has k possible outcomes, with each outcome having an equal chance of occurrence (1/6). However, dice rolls can also be converted into a binomial experiment; for example, by defining success as rolling a specific number, such as 6, and failure as not rolling the target number.
In this context, the binomial probability and the binomial distribution calculator can be employed to compute the probabilities of various events and the expected values related to dice rolls. For instance, one might calculate the probability of rolling a 6 twice in 10 tosses or the chance of rolling at least one 6 in 10 tosses.
When working with dice rolls, it's important to consider the discrete distribution, as there is a finite number of possible outcomes. The binomial probability function serves to provide an accurate probability distribution for dice roll experiments, allowing for the analysis and interpretation of the results.
In summary, binomial probability calculators and the concepts related to binomial distributions are crucial in addressing questions and problems related to coin tosses and dice rolls. These tools and concepts aid in accurately analyzing the data and understanding the nature of such probabilistic experiments.
Other Tools: P Value From Z Score , P Value From T Score , Confidence Interval (proportion) , t critical value calculator , z critical value calculator
Informative
Conversion Calculator
Follow Us On:
Binomial Distribution Calculator
Enter the number of trials and successes, probability, and select condition to calculate probability of the event accordingly, standard deviation, variance, mean, with detailed calculations and graphical interpretaton displayed.
Add this calculator to your site
An online Binomial Distribution Calculator can find the cumulative and binomial probabilities for the given values. Now, you can determine the standard deviation, variance, and mean of the binomial distribution quickly with a binomial probability distribution calculator. In the following article, you can understand what exactly is the binomial distribution, when and how to apply it, and much more information that you should know about the probability distribution. Let’s begin with some basics!
What is Binomial Distribution?
In statistics, the binomial distribution is a discrete probability distribution that only gives two possible results in an experiment either failure or success. For example, if we toss with a coin, there can only be two possible outcomes: tails or heads, and when taking any test, there can only be two outcomes: pass or fail. This distribution is called the binomial probability distribution.
Two parameters p and n are used in the binomial distribution. The variable "n" represents the frequency of the experiment, and the variable "p" represents the probability of the result. Assuming that the dice is randomly rolled 10 times, then the probability of each roll is 2. If you roll the dice 10 times, you will get a binomial distribution with p = ⅙ and n = 10.
Explore the formula for calculating the distribution of two results in multiple experiments.
Binomial Distribution Formula:
The formula for the binomial distribution is:
$$ P(x) = pr (1 − p) n−r . nCr $$
$$ P(x) = pr (1 − p) n−r . [n!/r!(n−r)!] $$
r = Total number of successful trails
n = Total number of events
p = Probability of success
1 – p = Probability of failure
nCr = [n!/r!(n−r)]!
However, an online Poisson Distribution Calculator determines the probability of the event happening many times over some given intervals.
How to Calculate Binomial Probability Distribution?
Here’s a comprehensive example that describes how a binomial distribution calculator works which can be helpful for determining the binomial distribution manually if required.
A coin is tossed 5 times with 0.13 probability for the number of successes (x) and the condition with exactly X success P(X = x).
Probability of exactly 3 successes
$$P(X = 3) = 0.016629093$$
Use a binomial CDF calculator to get the standard deviation, variance, and mean of binomial distribution based on the number of trails you provided.
Mean: μ = np = ((5) × (0.13)) = 0.65
Variance: σ2 = np (1 − p) = (5) (0.13) (1 − 0.13) = 0.5655
Standard deviation: σ = np(1 − p) = (5) (0.13) (1 − 0.13) = 0.75199734042083
Given Values :
Trials =5, p = 0.13 and X = 3
$$ P(X) = (nX) ⋅ pX ⋅ (1 − p)^{n – X} $$
The binomial coefficient, (nX) is defined by:
$$ (nX) = n! / X! (n−X)! $$
The binomial probability formula that is used by the binomial probability calculator with the binomial coefficient is:
$$ P(X) = n! / X! (n − X)! ⋅ p^X⋅ (1 − p) n − X $$
n = number of trials
p = probability of success on a single trial,
X = number of successes
Substituting in values for this problem, n = 5, p = 0.13 and X = 3:
$$ P (3) = 5! / 3! (5−3)! ⋅ 0.133 ⋅ (1 − 0.13) 5 − 3 $$
After Solving the expression:
$$ P (3) = 0.016629093 $$
The Binomial Distribution Calculator Provide a table for: n = 5, p = 0.13
$$ P(0) = 0.4984209207 $$
$$ P(1) = 0.3723834465 $$
$$ P(2) = 0.111287007 $$
$$ P(3) = 0.016629093 $$
$$ P(4) = 0.0012424035 $$
$$ P(5) = 3.71293E−5 $$
Pie Chart for Probability Relative:
The binomial probability calculator displays a pie chart for probability relative:
.webp)
Probability vs Number of successes Graph:
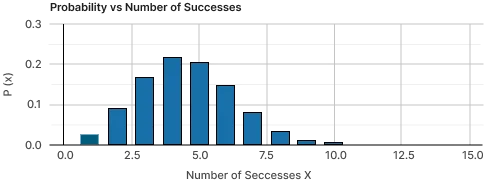
However, an online Binomial Theorem Calculator helps you to find the expanding binomials for the given binomial equation.
Binomial Probability Distribution:
In the probability distribution, the number of "successes" in the sequence of n experiments, where every time is asking for "yes or no", then the result is expressed as a Boolean value for success/Yes/ True/probability p or failure/no/false/probability q = 1-p.
The successful/failed unit test is also called the Bernoulli test or Bernoulli experiment and the series of results is called the Bernoulli process.
For n = 1 that is for a single experiment, the binomial distribution is the Bernoulli distribution. The binomial distribution is the basis of the famous binomial statistical significance test.
Negative Binomial Distribution:
In probability, the number of successful results in a series of identically distributed and independent distributed Bernoulli tests before a certain number of failures occur. This is called a negative binomial distribution. The number of failures/errors is represented by the letter "r".
Binomial Distribution Mean and Variance:
For the binomial distribution, the variance, mean, and standard deviation of a given number of successes are expressed by the following formula
$$ Variance, σ2 = npq $$
$$ Mean, μ = np $$
$$ Standard Deviation σ= √(npq) $$
These formulae are used by a binomial distribution calculator for determining the variance, mean, and standard deviation.
p = probability of success
q = probability of failure
Binomial and Normal Distribution:
The main difference between the normal distribution and the binomial distribution is that the binomial distribution is discrete, while the normal distribution is continuous. It means the binomial distribution is the limited number of events whereas the normal distribution has an infinite number of events. If the sample size of the binomial distribution is very large, then the distribution curve of the binomial distribution is the same as the normal distribution curve.
Properties of Binomial Distribution:
The main properties of the binomial distribution are:
- There are two possible outcomes: success or failure, true or false, yes or no.
- There is 'n' fixed number of n repeated attempts or the independent trails.
- Each trail has a different probability of failure or success.
- Only count the number of successes n that are independent trials.
- Each test is an independent trial that means the result of one trial has no effect on the result of another trial.
How does Binomial Distribution Calculator Works?
An online binomial probability distribution calculator finds the probabilities for different conditions by using these steps:
- First, enter the number of trails, probability, and the number of successes.
- Now, choose the condition for determining the binomial distribution.
- Click on the Calculate button.
- The binomial probability formula calculator displays the variance, mean, and standard deviation.
- An online binomial calculator shows the binomial coefficients, binomial distribution table, pie chart, and bar graph for probability and number of success.
What are the criteria of binomial distribution?
- The number of trials/tests should be specified.
- Each trial must be independent.
- The probability of success in each trial is the same.
Uses of Binomial Distribution in real life.
In real life, you can find many examples of binomial distributions. For example, when a new medicine is used to treat a disease, it either cures the disease (which is successful) or cannot cure the disease (which is a failure).
Conclusion:
Use this online binomial distribution calculator to evaluate the cumulative probabilities for the binomial distribution, given the number of trials (n), the number of success (X), and the probability (p) of the successful outcomes occurring. It also computes the variance, mean of binomial distribution, and standard deviation with different graphs.
From the source of Wikipedia: Probability mass function, Cumulative distribution function , Expected value and variance, Higher moments, Sums of binomials, Ratio of two binomial distributions. From the source of Investopedia: Analyzing Binomial Distribution, probability distribution , normal distribution, binomial distribution. From the source of Lumen Learning: Binomial Probability Distribution , Concept Review, Formula Review.
Poisson Distribution Calculator
Binomial Theorem Calculator
Coin Flip Calculator
Mean Median Mode Range Calculator
Percentage Increase Calculator
Probability Density Function Calculator
Covariance Calculator
Add this calculator to your site.
Just copy a given code & paste it right now into your website HTML (source) for suitable page.
Give Us Your Feedback

Share Result

Get the ease of calculating anything from the source of calculator online
Email us at
© Copyrights 2024 by Calculator-Online.net
CTRL Calculator - 4000+ Problem Solving Free Online Calculators
Binomial Probability Distribution Calculator
Enter the values in binomial probability distribution calculator to compute probabilities in scenarios involving a fixed number of independent trials, each with two possible outcomes: success or failure.
| n (trials) | p (probability) | k (successes) | P(X = k) | P(X ≤ k) |
|---|---|---|---|---|
| 10 | 0.5 | 5 | 0.2461 | 0.6230 |
| 20 | 0.3 | 6 | 0.2066 | 0.8670 |
| 15 | 0.7 | 10 | 0.1948 | 0.8479 |
| 30 | 0.4 | 12 | 0.1658 | 0.5535 |
| 50 | 0.6 | 35 | 0.0364 | 0.9780 |
Explanation of calculations:
- n = 10, p = 0.5, k = 5: This represents flipping a fair coin 10 times and getting exactly 5 heads.
- n = 20, p = 0.3, k = 6: This could represent a production line where each item has a 30% chance of being defective, and we’re calculating the probability of exactly 6 defective items in a batch of 20.
- n = 15, p = 0.7, k = 10: This might represent a basketball player with a 70% free throw percentage, calculating the probability of making exactly 10 out of 15 free throws.
- n = 30, p = 0.4, k = 12: This could represent a marketing campaign where each customer has a 40% chance of conversion, calculating the probability of exactly 12 conversions out of 30 customers.
- n = 50, p = 0.6, k = 35: This might represent a quality control scenario where each product has a 60% chance of passing inspection, calculating the probability of exactly 35 products passing out of 50.
More Calculators : – Expected Value Calculator – Shannon Entropy Calculator
Binomial Distribution Probability Calculation Formula
The formula for calculating the probability of exactly k successes in n trials is:
P(X = k) = C(n,k) * p^k * (1-p)^(n-k)
- P(X = k) is the probability of exactly k successes
- C(n,k) is the number of ways to choose k items from n items (combination)
- p is the probability of success on each trial
- n is the total number of trials
- k is the number of successes we’re interested in
The combination C(n,k) is calculated as:
C(n,k) = n! / (k! * (n-k)!)
Where ! denotes the factorial operation.
What is the cumulative probability of a binomial?
The cumulative probability of a binomial distribution refers to the probability of obtaining up to and including a certain number of successes.
It is often denoted as P(X ≤ k) , which means the probability of getting k or fewer successes in n trials.
To calculate the cumulative probability, we sum the individual probabilities for all outcomes from 0 to k:
P(X ≤ k) = P(X = 0) + P(X = 1) + P(X = 2) + … + P(X = k)
This calculation can be tedious for large values of n and k, which is why binomial probability distribution calculators are invaluable.
They can quickly compute both individual and cumulative probabilities for various combinations of n, p, and k.
What is the probability of success in n trials?
The probability of success in n trials can have two interpretations:
- Probability of at least one success : This is often what people mean when they ask about the probability of success in n trials. It’s calculated as the complement of the probability of no successes: P(at least one success) = 1 – P(X = 0) = 1 – (1-p)^n
- Expected number of successes : This is the average number of successes you’d expect to see if you repeated the n trials many times. It’s calculated as: E(X) = n * p
For example, if you flip a fair coin (p = 0.5) 10 times (n = 10):
- The probability of getting at least one heads is: 1 – (1-0.5)^10 ≈ 0.999 (99.9%)
- The expected number of heads is: 10 * 0.5 = 5
Binomial Distribution TI 84
The TI-84 is a popular graphing calculator that includes built-in functions for working with binomial distributions. Here’s how you can use the TI-84 for binomial distribution calculations:
- This function calculates P(X = k)
- Syntax: binompdf(n, p, k)
- Access: Press [2nd] [DISTR], then select 0:binompdf(
- Example: To calculate the probability of exactly 5 successes in 10 trials with p = 0.5, enter binompdf(10, 0.5, 5)
- This function calculates P(X ≤ k)
- Syntax: binomcdf(n, p, k)
- Access: Press [2nd] [DISTR], then select A:binomcdf(
- Example: To calculate the probability of 5 or fewer successes in 10 trials with p = 0.5, enter binomcdf(10, 0.5, 5)
- You can also graph the binomial distribution on the TI-84
- Enter the stat plot menu by pressing [2nd] [Y=]
- Select a plot and set it to histogram or bar graph
- Use binompdf(n, p, X) as the Xlist and leave Freq as 1
- Adjust your window settings and graph
Using the TI-84 for binomial distribution calculations can significantly speed up your work, especially for larger values of n and k. It’s particularly useful for students in statistics classes and professionals who need quick probability calculations in the field.
Related Tools:
- Dice Roller Calculator
- Delay and Reverb Calculator
- Roulette Payout Calculator
- Bending Stress Calculator
- Caffeine Half-Life Calculator
- Dog Grape Toxicity Calculator
Thanks for visiting and reading! My name is Garth, and I would like to welcome you to my personal birding space.
Similar Posts
Roulette payout calculator free online, dice roller calculator – virtual dice probability calculation, shannon entropy calculator and formula, polynomial regression calculator, sensitivity and specificity calculator, expected value calculator | formula and examples, leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Binomial Distribution Calculator
Enter the probability of success for a single trial, the number of trials, and the number of successes to calculate the binomial and cumulative probabilities of getting successful events.
Have a Question or Feedback?
Probabilities:.
| P(X = x): | |
|---|---|
| P(X < x): | |
| P(X ≤ x): | |
| P(X > x): | |
| P(X ≥ x): |
Chevron Down Icon scroll down
On this page:
How to calculate a binomial distribution, how to calculate a binomial probability, binomial probability formula, binomial probability distribution table, how to calculate cumulative binomial probabilities, binomial cumulative distribution function, frequently asked questions.

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Full bio Chevron Right Icon

Brian specializes in political science and statistics with several advanced degrees from Harvard.

Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
In statistics , a binomial distribution is a probability distribution of the number of successes in a sequence of independent experiments or trials. The result of each experiment must be dichotomous, which means the result must be a yes/no, success/fail, heads/tails, true/false, or similar outcome.
Unlike a normal distribution , a binomial distribution is a probability distribution for a discrete variable, while a normal distribution describes a continuous variable. Binomial distributions can be skewed or symmetrical, while a normal distribution is always symmetrical.
Each experiment in a sequence is referred to as a trial, or more specifically, a Bernoulli trial. The sequence is sometimes referred to as a Bernoulli process, named for mathematician Jacob Bernoulli.
The binomial distribution describes the likelihood of possible outcomes from a set of trials.
To help better understand the binomial distribution, let’s use the example of recording coin flips. Let’s say we ran a sequence of 100 coin flips and measured the number of times it landed on heads. If we repeated this sequence of one hundred flips 20,000 times and plotted the number of heads in each sequence, we might see a distribution like this one.
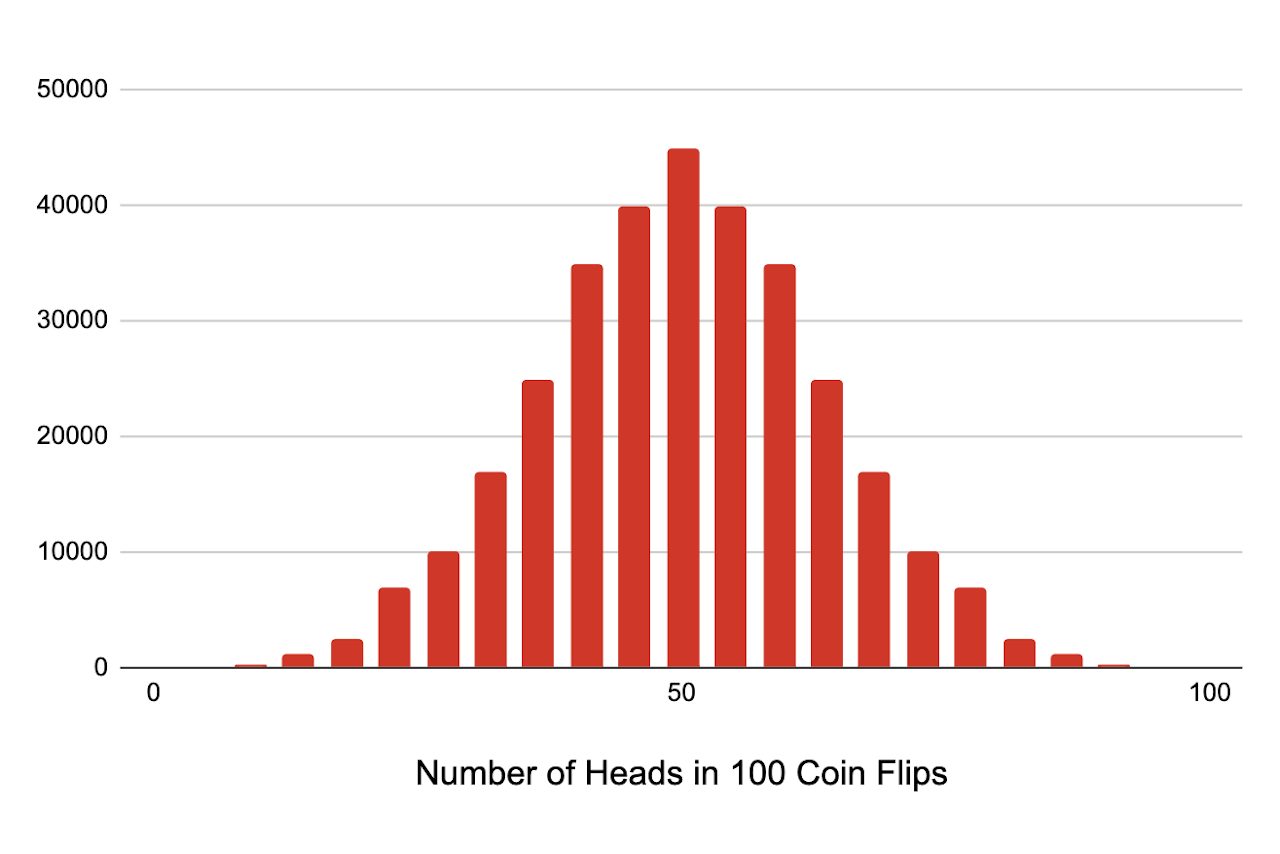
In this sequence, the number of trials n is 100, representing the 100 coin flips. The number of successes x is the number of times in the sequence that the coin landed on heads. The probability p is 0.5 since there is a 50% chance of landing on heads.
A binomial probability is the probability of getting exactly x successes in a sequence of n trials, where the probability p of success in each trial is the same. Each trial must be independent, meaning that the results of one trial do not influence the probability that the next trial will be successful.
There are a few ways to calculate a binomial probability. The first method is to use a formula, and the second is to refer to a binomial probability distribution chart.
You can calculate the binomial probability using the binomial probability mass function: [1]
The binomial probability mass function (PMF) states that the probability of x successes in a sequence of n independent trials with a probability of success in a single trial p is equal to the number of possible combinations of success times p to the power of x times 1 minus p to the power of n minus x .
You may also see the probability mass function referred to as the binomial probability density function (PDF). But, because a binomial distribution is a distribution of a discrete variable rather than a continuous variable, it is technically a mass function, not a density function.
You can calculate the number of possible combinations using our combinations calculator . The number of combinations can also be found using the formula:
The number of combinations is equal to the number of events or trials n factorial divided by the number of successes x factorial times n minus x factorial. Our factorial calculator might be useful for this calculation.

The binomial distribution table below shows the probability of getting x successes in a sample of n trials, with a probability of success in each trial p .
| p | ||||||||||||
| x | 0.05 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 0.95 | |
| n = 1 | 0 | 0.950 | 0.900 | 0.800 | 0.700 | 0.600 | 0.500 | 0.400 | 0.300 | 0.200 | 0.100 | 0.050 |
| 1 | 0.050 | 0.100 | 0.200 | 0.300 | 0.400 | 0.500 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 | |
| n = 2 | 0 | 0.903 | 0.810 | 0.640 | 0.490 | 0.360 | 0.250 | 0.160 | 0.090 | 0.040 | 0.010 | 0.003 |
| 1 | 0.095 | 0.180 | 0.320 | 0.420 | 0.480 | 0.500 | 0.480 | 0.420 | 0.320 | 0.180 | 0.095 | |
| 2 | 0.003 | 0.010 | 0.040 | 0.090 | 0.160 | 0.250 | 0.360 | 0.490 | 0.640 | 0.810 | 0.903 | |
| n = 3 | 0 | 0.857 | 0.729 | 0.512 | 0.343 | 0.216 | 0.125 | 0.064 | 0.027 | 0.008 | 0.001 | 0.000 |
| 1 | 0.135 | 0.243 | 0.384 | 0.441 | 0.432 | 0.375 | 0.288 | 0.189 | 0.096 | 0.027 | 0.007 | |
| 2 | 0.007 | 0.027 | 0.096 | 0.189 | 0.288 | 0.375 | 0.432 | 0.441 | 0.384 | 0.243 | 0.135 | |
| 3 | 0.000 | 0.001 | 0.008 | 0.027 | 0.064 | 0.125 | 0.216 | 0.343 | 0.512 | 0.729 | 0.857 | |
| n = 4 | 0 | 0.815 | 0.656 | 0.410 | 0.240 | 0.130 | 0.063 | 0.026 | 0.008 | 0.002 | 0.000 | 0.000 |
| 1 | 0.171 | 0.292 | 0.410 | 0.412 | 0.346 | 0.250 | 0.154 | 0.076 | 0.026 | 0.004 | 0.000 | |
| 2 | 0.014 | 0.049 | 0.154 | 0.265 | 0.346 | 0.375 | 0.346 | 0.265 | 0.154 | 0.049 | 0.014 | |
| 3 | 0.000 | 0.004 | 0.026 | 0.076 | 0.154 | 0.250 | 0.346 | 0.412 | 0.410 | 0.292 | 0.171 | |
| 4 | 0.000 | 0.000 | 0.002 | 0.008 | 0.026 | 0.063 | 0.130 | 0.240 | 0.410 | 0.656 | 0.815 | |
| n = 5 | 0 | 0.774 | 0.590 | 0.328 | 0.168 | 0.078 | 0.031 | 0.010 | 0.002 | 0.000 | 0.000 | 0.000 |
| 1 | 0.204 | 0.328 | 0.410 | 0.360 | 0.259 | 0.156 | 0.077 | 0.028 | 0.006 | 0.000 | 0.000 | |
| 2 | 0.021 | 0.073 | 0.205 | 0.309 | 0.346 | 0.313 | 0.230 | 0.132 | 0.051 | 0.008 | 0.001 | |
| 3 | 0.001 | 0.008 | 0.051 | 0.132 | 0.230 | 0.313 | 0.346 | 0.309 | 0.205 | 0.073 | 0.021 | |
| 4 | 0.000 | 0.000 | 0.006 | 0.028 | 0.077 | 0.156 | 0.259 | 0.360 | 0.410 | 0.328 | 0.204 | |
| 5 | 0.000 | 0.000 | 0.000 | 0.002 | 0.010 | 0.031 | 0.078 | 0.168 | 0.328 | 0.590 | 0.774 | |
| n = 6 | 0 | 0.735 | 0.531 | 0.262 | 0.118 | 0.047 | 0.016 | 0.004 | 0.001 | 0.000 | 0.000 | 0.000 |
| 1 | 0.232 | 0.354 | 0.393 | 0.303 | 0.187 | 0.094 | 0.037 | 0.010 | 0.002 | 0.000 | 0.000 | |
| 2 | 0.031 | 0.098 | 0.246 | 0.324 | 0.311 | 0.234 | 0.138 | 0.060 | 0.015 | 0.001 | 0.000 | |
| 3 | 0.002 | 0.015 | 0.082 | 0.185 | 0.276 | 0.313 | 0.276 | 0.185 | 0.082 | 0.015 | 0.002 | |
| 4 | 0.000 | 0.001 | 0.015 | 0.060 | 0.138 | 0.234 | 0.311 | 0.324 | 0.246 | 0.098 | 0.031 | |
| 5 | 0.000 | 0.000 | 0.002 | 0.010 | 0.037 | 0.094 | 0.187 | 0.303 | 0.393 | 0.354 | 0.232 | |
| 6 | 0.000 | 0.000 | 0.000 | 0.001 | 0.004 | 0.016 | 0.047 | 0.118 | 0.262 | 0.531 | 0.735 | |
| n = 7 | 0 | 0.698 | 0.478 | 0.210 | 0.082 | 0.028 | 0.008 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.257 | 0.372 | 0.367 | 0.247 | 0.131 | 0.055 | 0.017 | 0.004 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.041 | 0.124 | 0.275 | 0.318 | 0.261 | 0.164 | 0.077 | 0.025 | 0.004 | 0.000 | 0.000 | |
| 3 | 0.004 | 0.023 | 0.115 | 0.227 | 0.290 | 0.273 | 0.194 | 0.097 | 0.029 | 0.003 | 0.000 | |
| 4 | 0.000 | 0.003 | 0.029 | 0.097 | 0.194 | 0.273 | 0.290 | 0.227 | 0.115 | 0.023 | 0.004 | |
| 5 | 0.000 | 0.000 | 0.004 | 0.025 | 0.077 | 0.164 | 0.261 | 0.318 | 0.275 | 0.124 | 0.041 | |
| 6 | 0.000 | 0.000 | 0.000 | 0.004 | 0.017 | 0.055 | 0.131 | 0.247 | 0.367 | 0.372 | 0.257 | |
| 7 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.008 | 0.028 | 0.082 | 0.210 | 0.478 | 0.698 | |
| n = 8 | 0 | 0.663 | 0.430 | 0.168 | 0.058 | 0.017 | 0.004 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.279 | 0.383 | 0.336 | 0.198 | 0.090 | 0.031 | 0.008 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.051 | 0.149 | 0.294 | 0.296 | 0.209 | 0.109 | 0.041 | 0.010 | 0.001 | 0.000 | 0.000 | |
| 3 | 0.005 | 0.033 | 0.147 | 0.254 | 0.279 | 0.219 | 0.124 | 0.047 | 0.009 | 0.000 | 0.000 | |
| 4 | 0.000 | 0.005 | 0.046 | 0.136 | 0.232 | 0.273 | 0.232 | 0.136 | 0.046 | 0.005 | 0.000 | |
| 5 | 0.000 | 0.000 | 0.009 | 0.047 | 0.124 | 0.219 | 0.279 | 0.254 | 0.147 | 0.033 | 0.005 | |
| 6 | 0.000 | 0.000 | 0.001 | 0.010 | 0.041 | 0.109 | 0.209 | 0.296 | 0.294 | 0.149 | 0.051 | |
| 7 | 0.000 | 0.000 | 0.000 | 0.001 | 0.008 | 0.031 | 0.090 | 0.198 | 0.336 | 0.383 | 0.279 | |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.004 | 0.017 | 0.058 | 0.168 | 0.430 | 0.663 | |
| n = 9 | 0 | 0.630 | 0.387 | 0.134 | 0.040 | 0.010 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.299 | 0.387 | 0.302 | 0.156 | 0.060 | 0.018 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.063 | 0.172 | 0.302 | 0.267 | 0.161 | 0.070 | 0.021 | 0.004 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.008 | 0.045 | 0.176 | 0.267 | 0.251 | 0.164 | 0.074 | 0.021 | 0.003 | 0.000 | 0.000 | |
| 4 | 0.001 | 0.007 | 0.066 | 0.172 | 0.251 | 0.246 | 0.167 | 0.074 | 0.017 | 0.001 | 0.000 | |
| 5 | 0.000 | 0.001 | 0.017 | 0.074 | 0.167 | 0.246 | 0.251 | 0.172 | 0.066 | 0.007 | 0.001 | |
| 6 | 0.000 | 0.000 | 0.003 | 0.021 | 0.074 | 0.164 | 0.251 | 0.267 | 0.176 | 0.045 | 0.008 | |
| 7 | 0.000 | 0.000 | 0.000 | 0.004 | 0.021 | 0.070 | 0.161 | 0.267 | 0.302 | 0.172 | 0.063 | |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.018 | 0.060 | 0.156 | 0.302 | 0.387 | 0.299 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.010 | 0.040 | 0.134 | 0.387 | 0.630 | |
| n = 10 | 0 | 0.599 | 0.349 | 0.107 | 0.028 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.315 | 0.387 | 0.268 | 0.121 | 0.040 | 0.010 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.075 | 0.194 | 0.302 | 0.233 | 0.121 | 0.044 | 0.011 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.010 | 0.057 | 0.201 | 0.267 | 0.215 | 0.117 | 0.042 | 0.009 | 0.001 | 0.000 | 0.000 | |
| 4 | 0.001 | 0.011 | 0.088 | 0.200 | 0.251 | 0.205 | 0.111 | 0.037 | 0.006 | 0.000 | 0.000 | |
| 5 | 0.000 | 0.001 | 0.026 | 0.103 | 0.201 | 0.246 | 0.201 | 0.103 | 0.026 | 0.001 | 0.000 | |
| 6 | 0.000 | 0.000 | 0.006 | 0.037 | 0.111 | 0.205 | 0.251 | 0.200 | 0.088 | 0.011 | 0.001 | |
| 7 | 0.000 | 0.000 | 0.001 | 0.009 | 0.042 | 0.117 | 0.215 | 0.267 | 0.201 | 0.057 | 0.010 | |
| 8 | 0.000 | 0.000 | 0.000 | 0.001 | 0.011 | 0.044 | 0.121 | 0.233 | 0.302 | 0.194 | 0.075 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.010 | 0.040 | 0.121 | 0.268 | 0.387 | 0.315 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.006 | 0.028 | 0.107 | 0.349 | 0.599 | |
| n = 11 | 0 | 0.569 | 0.314 | 0.086 | 0.020 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.329 | 0.384 | 0.236 | 0.093 | 0.027 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.087 | 0.213 | 0.295 | 0.200 | 0.089 | 0.027 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.014 | 0.071 | 0.221 | 0.257 | 0.177 | 0.081 | 0.023 | 0.004 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.001 | 0.016 | 0.111 | 0.220 | 0.236 | 0.161 | 0.070 | 0.017 | 0.002 | 0.000 | 0.000 | |
| 5 | 0.000 | 0.002 | 0.039 | 0.132 | 0.221 | 0.226 | 0.147 | 0.057 | 0.010 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.000 | 0.010 | 0.057 | 0.147 | 0.226 | 0.221 | 0.132 | 0.039 | 0.002 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.002 | 0.017 | 0.070 | 0.161 | 0.236 | 0.220 | 0.111 | 0.016 | 0.001 | |
| 8 | 0.000 | 0.000 | 0.000 | 0.004 | 0.023 | 0.081 | 0.177 | 0.257 | 0.221 | 0.071 | 0.014 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.001 | 0.005 | 0.027 | 0.089 | 0.200 | 0.295 | 0.213 | 0.087 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.005 | 0.027 | 0.093 | 0.236 | 0.384 | 0.329 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.020 | 0.086 | 0.314 | 0.569 | |
| n = 12 | 0 | 0.540 | 0.282 | 0.069 | 0.014 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.341 | 0.377 | 0.206 | 0.071 | 0.017 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.099 | 0.230 | 0.283 | 0.168 | 0.064 | 0.016 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.017 | 0.085 | 0.236 | 0.240 | 0.142 | 0.054 | 0.012 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.002 | 0.021 | 0.133 | 0.231 | 0.213 | 0.121 | 0.042 | 0.008 | 0.001 | 0.000 | 0.000 | |
| 5 | 0.000 | 0.004 | 0.053 | 0.158 | 0.227 | 0.193 | 0.101 | 0.029 | 0.003 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.000 | 0.016 | 0.079 | 0.177 | 0.226 | 0.177 | 0.079 | 0.016 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.003 | 0.029 | 0.101 | 0.193 | 0.227 | 0.158 | 0.053 | 0.004 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.001 | 0.008 | 0.042 | 0.121 | 0.213 | 0.231 | 0.133 | 0.021 | 0.002 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.001 | 0.012 | 0.054 | 0.142 | 0.240 | 0.236 | 0.085 | 0.017 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.016 | 0.064 | 0.168 | 0.283 | 0.230 | 0.099 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.017 | 0.071 | 0.206 | 0.377 | 0.341 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.014 | 0.069 | 0.282 | 0.540 | |
| n = 13 | 0 | 0.513 | 0.254 | 0.055 | 0.010 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.351 | 0.367 | 0.179 | 0.054 | 0.011 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.111 | 0.245 | 0.268 | 0.139 | 0.045 | 0.010 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.021 | 0.100 | 0.246 | 0.218 | 0.111 | 0.035 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.003 | 0.028 | 0.154 | 0.234 | 0.184 | 0.087 | 0.024 | 0.003 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.000 | 0.006 | 0.069 | 0.180 | 0.221 | 0.157 | 0.066 | 0.014 | 0.001 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.001 | 0.023 | 0.103 | 0.197 | 0.209 | 0.131 | 0.044 | 0.006 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.006 | 0.044 | 0.131 | 0.209 | 0.197 | 0.103 | 0.023 | 0.001 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.001 | 0.014 | 0.066 | 0.157 | 0.221 | 0.180 | 0.069 | 0.006 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.003 | 0.024 | 0.087 | 0.184 | 0.234 | 0.154 | 0.028 | 0.003 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.001 | 0.006 | 0.035 | 0.111 | 0.218 | 0.246 | 0.100 | 0.021 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.010 | 0.045 | 0.139 | 0.268 | 0.245 | 0.111 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.011 | 0.054 | 0.179 | 0.367 | 0.351 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.010 | 0.055 | 0.254 | 0.513 | |
| n = 14 | 0 | 0.488 | 0.229 | 0.044 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.359 | 0.356 | 0.154 | 0.041 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.123 | 0.257 | 0.250 | 0.113 | 0.032 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.026 | 0.114 | 0.250 | 0.194 | 0.085 | 0.022 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.004 | 0.035 | 0.172 | 0.229 | 0.155 | 0.061 | 0.014 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.000 | 0.008 | 0.086 | 0.196 | 0.207 | 0.122 | 0.041 | 0.007 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.001 | 0.032 | 0.126 | 0.207 | 0.183 | 0.092 | 0.023 | 0.002 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.009 | 0.062 | 0.157 | 0.209 | 0.157 | 0.062 | 0.009 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.002 | 0.023 | 0.092 | 0.183 | 0.207 | 0.126 | 0.032 | 0.001 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.000 | 0.007 | 0.041 | 0.122 | 0.207 | 0.196 | 0.086 | 0.008 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.001 | 0.014 | 0.061 | 0.155 | 0.229 | 0.172 | 0.035 | 0.004 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.022 | 0.085 | 0.194 | 0.250 | 0.114 | 0.026 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.006 | 0.032 | 0.113 | 0.250 | 0.257 | 0.123 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.007 | 0.041 | 0.154 | 0.356 | 0.359 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.007 | 0.044 | 0.229 | 0.488 | |
| n = 15 | 0 | 0.463 | 0.206 | 0.035 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.366 | 0.343 | 0.132 | 0.031 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.135 | 0.267 | 0.231 | 0.092 | 0.022 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.031 | 0.129 | 0.250 | 0.170 | 0.063 | 0.014 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.005 | 0.043 | 0.188 | 0.219 | 0.127 | 0.042 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.001 | 0.010 | 0.103 | 0.206 | 0.186 | 0.092 | 0.024 | 0.003 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.002 | 0.043 | 0.147 | 0.207 | 0.153 | 0.061 | 0.012 | 0.001 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.014 | 0.081 | 0.177 | 0.196 | 0.118 | 0.035 | 0.003 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.003 | 0.035 | 0.118 | 0.196 | 0.177 | 0.081 | 0.014 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.001 | 0.012 | 0.061 | 0.153 | 0.207 | 0.147 | 0.043 | 0.002 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.003 | 0.024 | 0.092 | 0.186 | 0.206 | 0.103 | 0.010 | 0.001 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.001 | 0.007 | 0.042 | 0.127 | 0.219 | 0.188 | 0.043 | 0.005 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.014 | 0.063 | 0.170 | 0.250 | 0.129 | 0.031 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.022 | 0.092 | 0.231 | 0.267 | 0.135 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.031 | 0.132 | 0.343 | 0.366 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.035 | 0.206 | 0.463 | |
| n = 16 | 0 | 0.440 | 0.185 | 0.028 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.371 | 0.329 | 0.113 | 0.023 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.146 | 0.275 | 0.211 | 0.073 | 0.015 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.036 | 0.142 | 0.246 | 0.146 | 0.047 | 0.009 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.006 | 0.051 | 0.200 | 0.204 | 0.101 | 0.028 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.001 | 0.014 | 0.120 | 0.210 | 0.162 | 0.067 | 0.014 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.003 | 0.055 | 0.165 | 0.198 | 0.122 | 0.039 | 0.006 | 0.000 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.000 | 0.020 | 0.101 | 0.189 | 0.175 | 0.084 | 0.019 | 0.001 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.006 | 0.049 | 0.142 | 0.196 | 0.142 | 0.049 | 0.006 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.001 | 0.019 | 0.084 | 0.175 | 0.189 | 0.101 | 0.020 | 0.000 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.006 | 0.039 | 0.122 | 0.198 | 0.165 | 0.055 | 0.003 | 0.000 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.001 | 0.014 | 0.067 | 0.162 | 0.210 | 0.120 | 0.014 | 0.001 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.028 | 0.101 | 0.204 | 0.200 | 0.051 | 0.006 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.009 | 0.047 | 0.146 | 0.246 | 0.142 | 0.036 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.015 | 0.073 | 0.211 | 0.275 | 0.146 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.023 | 0.113 | 0.329 | 0.371 | |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.028 | 0.185 | 0.440 | |
| n = 17 | 0 | 0.418 | 0.167 | 0.023 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.374 | 0.315 | 0.096 | 0.017 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.158 | 0.280 | 0.191 | 0.058 | 0.010 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.041 | 0.156 | 0.239 | 0.125 | 0.034 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.008 | 0.060 | 0.209 | 0.187 | 0.080 | 0.018 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.001 | 0.017 | 0.136 | 0.208 | 0.138 | 0.047 | 0.008 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.004 | 0.068 | 0.178 | 0.184 | 0.094 | 0.024 | 0.003 | 0.000 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.001 | 0.027 | 0.120 | 0.193 | 0.148 | 0.057 | 0.009 | 0.000 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.008 | 0.064 | 0.161 | 0.185 | 0.107 | 0.028 | 0.002 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.002 | 0.028 | 0.107 | 0.185 | 0.161 | 0.064 | 0.008 | 0.000 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.000 | 0.009 | 0.057 | 0.148 | 0.193 | 0.120 | 0.027 | 0.001 | 0.000 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.003 | 0.024 | 0.094 | 0.184 | 0.178 | 0.068 | 0.004 | 0.000 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.001 | 0.008 | 0.047 | 0.138 | 0.208 | 0.136 | 0.017 | 0.001 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.018 | 0.080 | 0.187 | 0.209 | 0.060 | 0.008 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.034 | 0.125 | 0.239 | 0.156 | 0.041 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.010 | 0.058 | 0.191 | 0.280 | 0.158 | |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.017 | 0.096 | 0.315 | 0.374 | |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.023 | 0.167 | 0.418 | |
| n = 18 | 0 | 0.397 | 0.150 | 0.018 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.376 | 0.300 | 0.081 | 0.013 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.168 | 0.284 | 0.172 | 0.046 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.047 | 0.168 | 0.230 | 0.105 | 0.025 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.009 | 0.070 | 0.215 | 0.168 | 0.061 | 0.012 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.001 | 0.022 | 0.151 | 0.202 | 0.115 | 0.033 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.005 | 0.082 | 0.187 | 0.166 | 0.071 | 0.015 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.001 | 0.035 | 0.138 | 0.189 | 0.121 | 0.037 | 0.005 | 0.000 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.012 | 0.081 | 0.173 | 0.167 | 0.077 | 0.015 | 0.001 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.003 | 0.039 | 0.128 | 0.185 | 0.128 | 0.039 | 0.003 | 0.000 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.001 | 0.015 | 0.077 | 0.167 | 0.173 | 0.081 | 0.012 | 0.000 | 0.000 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.005 | 0.037 | 0.121 | 0.189 | 0.138 | 0.035 | 0.001 | 0.000 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.001 | 0.015 | 0.071 | 0.166 | 0.187 | 0.082 | 0.005 | 0.000 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.033 | 0.115 | 0.202 | 0.151 | 0.022 | 0.001 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.012 | 0.061 | 0.168 | 0.215 | 0.070 | 0.009 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.025 | 0.105 | 0.230 | 0.168 | 0.047 | |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.007 | 0.046 | 0.172 | 0.284 | 0.168 | |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.013 | 0.081 | 0.300 | 0.376 | |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.018 | 0.150 | 0.397 | |
| n = 19 | 0 | 0.377 | 0.135 | 0.014 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.377 | 0.285 | 0.068 | 0.009 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.179 | 0.285 | 0.154 | 0.036 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.053 | 0.180 | 0.218 | 0.087 | 0.017 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.011 | 0.080 | 0.218 | 0.149 | 0.047 | 0.007 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.002 | 0.027 | 0.164 | 0.192 | 0.093 | 0.022 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.007 | 0.095 | 0.192 | 0.145 | 0.052 | 0.008 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.001 | 0.044 | 0.153 | 0.180 | 0.096 | 0.024 | 0.002 | 0.000 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.017 | 0.098 | 0.180 | 0.144 | 0.053 | 0.008 | 0.000 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.005 | 0.051 | 0.146 | 0.176 | 0.098 | 0.022 | 0.001 | 0.000 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.001 | 0.022 | 0.098 | 0.176 | 0.146 | 0.051 | 0.005 | 0.000 | 0.000 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.008 | 0.053 | 0.144 | 0.180 | 0.098 | 0.017 | 0.000 | 0.000 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.002 | 0.024 | 0.096 | 0.180 | 0.153 | 0.044 | 0.001 | 0.000 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.001 | 0.008 | 0.052 | 0.145 | 0.192 | 0.095 | 0.007 | 0.000 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.022 | 0.093 | 0.192 | 0.164 | 0.027 | 0.002 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.007 | 0.047 | 0.149 | 0.218 | 0.080 | 0.011 | |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.017 | 0.087 | 0.218 | 0.180 | 0.053 | |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.036 | 0.154 | 0.285 | 0.179 | |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.009 | 0.068 | 0.285 | 0.377 | |
| 19 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.014 | 0.135 | 0.377 | |
| n = 20 | 0 | 0.358 | 0.122 | 0.012 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 1 | 0.377 | 0.270 | 0.058 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 2 | 0.189 | 0.285 | 0.137 | 0.028 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0.060 | 0.190 | 0.205 | 0.072 | 0.012 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0.013 | 0.090 | 0.218 | 0.130 | 0.035 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 5 | 0.002 | 0.032 | 0.175 | 0.179 | 0.075 | 0.015 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 6 | 0.000 | 0.009 | 0.109 | 0.192 | 0.124 | 0.037 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 7 | 0.000 | 0.002 | 0.055 | 0.164 | 0.166 | 0.074 | 0.015 | 0.001 | 0.000 | 0.000 | 0.000 | |
| 8 | 0.000 | 0.000 | 0.022 | 0.114 | 0.180 | 0.120 | 0.035 | 0.004 | 0.000 | 0.000 | 0.000 | |
| 9 | 0.000 | 0.000 | 0.007 | 0.065 | 0.160 | 0.160 | 0.071 | 0.012 | 0.000 | 0.000 | 0.000 | |
| 10 | 0.000 | 0.000 | 0.002 | 0.031 | 0.117 | 0.176 | 0.117 | 0.031 | 0.002 | 0.000 | 0.000 | |
| 11 | 0.000 | 0.000 | 0.000 | 0.012 | 0.071 | 0.160 | 0.160 | 0.065 | 0.007 | 0.000 | 0.000 | |
| 12 | 0.000 | 0.000 | 0.000 | 0.004 | 0.035 | 0.120 | 0.180 | 0.114 | 0.022 | 0.000 | 0.000 | |
| 13 | 0.000 | 0.000 | 0.000 | 0.001 | 0.015 | 0.074 | 0.166 | 0.164 | 0.055 | 0.002 | 0.000 | |
| 14 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.037 | 0.124 | 0.192 | 0.109 | 0.009 | 0.000 | |
| 15 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.015 | 0.075 | 0.179 | 0.175 | 0.032 | 0.002 | |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.035 | 0.130 | 0.218 | 0.090 | 0.013 | |
| 17 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.012 | 0.072 | 0.205 | 0.190 | 0.060 | |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.028 | 0.137 | 0.285 | 0.189 | |
| 19 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.007 | 0.058 | 0.270 | 0.377 | |
| 20 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.012 | 0.122 | 0.358 | |
The binomial probability formula is useful to find the probability of exactly x successes in the sequence of n independent Bernoulli trials. However, sometimes you want to know the probability of no more than x successes, for instance.
This is referred to as the cumulative binomial probability, and you can find it using a cumulative distribution function.
If you want to know the probability of at least x successes, one uses the complementary cumulative distribution function, which is simply one minus the cumulative distribution function. Put differently, it is the chances of whatever is described by the cumulative distribution function NOT happening.
For example, if you want to know the probability of three or more heads in six coin flips, the only way that can fail to happen is if there are two or fewer heads. Supposing the coin is fair, the probability of 2 or fewer heads is approximately 0.34. Therefore, the probability of three or more heads is 1 – 0.34 or 0.66.
The cumulative distribution function to calculate cumulative binomial probabilities is: [2]
This is the binomial CDF that the calculator above uses to calculate the probabilities of getting less than or greater than x in the distribution.
You can contrast the binomial distribution with another commonly used discrete distribution, the Poisson distribution . While a binomial distribution is used to count the number of occurrences of some similar event among a finite set of trials, the Poisson distribution is used to count discrete occurrences where the rate of occurrences is known and so is the amount of time (or sometimes space) in which these events occur.
This description of the Poisson is a bit abstract. To take more concrete examples, the number of calls to a doctor’s office between 9 AM and 12 PM or meteor strikes in the ocean might be modeled using a Poisson distribution.

How do you know if something is a binomial distribution?
A binomial distribution will have results that will be a yes/no or a success/fail variable, where the probability of each result is identical, and where success or failure in one result does not influence the chances of success or failure in subsequent results. The latter property is called (statistical) independence.
When would you use a binomial distribution?
You would use a binomial distribution when there can only be two outcomes: success or failure.
What makes something not binomial?
Something would be not binomial if you could have more than two outcomes.
Is rolling a dice a binomial distribution?
No, rolling a dice is a normal distribution.
How could the probability of success or failure in one instance influence success in the next instance?
Statistical independence will often fail if outcomes are contingent on meeting some criteria. For example, drug trials may attempt to assign to treatment and control (placebo) based on a 50-50 coin-flip.
Naively assigning people to treatments based on coin flips will make it very likely that the study actually implemented will have an unequal number of people assigned to treatment and control. Possibly, it will be severely imbalanced with all individuals assigned to treatment (i.e. all heads) or all individuals assigned to control (i.e. all tails).
To avoid these kinds of experimental assignments, which would limit the study’s conclusions, study designers might only consider coin flips where the number of patients assigned to treatment or control is “good enough,” even requiring an equal number of treatments in treatment and control.
In doing so, they introduce a (negative) correlation between outcomes. To see why, suppose you know that there are 100 people to be included, and the study has assigned the first 50 patients to receive the treatment. Then you know the last 50 patients will be in control.
Indeed, if all you know is the first patient is assigned to treatment, and the overall treatment plan will have equal numbers in treatment and control, then it is a better than even money bet that the very next patient will get the placebo.
Recommended Statistics Resources
- Winning Percentage Calculator Right Arrow Icon
- Standard Error Calculator Right Arrow Icon
- Average Calculator Right Arrow Icon
- Central Limit Theorem Calculator Right Arrow Icon
- T-Test Calculator Right Arrow Icon
- Mohr, D., Binomial Probability Distribution, Science Direct , https://www.sciencedirect.com/topics/mathematics/binomial-probability-distribution
- National Institute of Standards and Technology, Exploratory Data Analysis - 1.3.6.6.18 Binomial Distribution, https://www.itl.nist.gov/div898/handbook/eda/section3/eda366i.htm
- Skip to the content.
- Skip to the primary sidebar.
- Statistics Calculators
- Binomial Probability Calculator
This online binomial probability calculator computes the probability of an exact binomial outcome (a binomial probability P ), given the number of trials n , the number of successes k , and the probability of the successful outcome of a single trial p . You can also compute cumulative binomial probabilities P for no more than k successes or for no less than k successes. The parameters n and k must be non-negative integers in the range of 0 ≤ k ≤ n .
Precision: decimal places
Exactly “k” successes No more than “k” successes No less than “k” successes
Binomial distribution formula
The binomial probability refers to the probability that a binomial experiment of \(n\) trials results in exactly \(k\) successes given each independent trial has the probability \(p\).
The binomial experiment (or Bernoulli experiment) is a statistical experiment that has the following four properties:
1. Fixed number of trials. 2. Each trial has only two possible outcomes (successes or failure). 3. Probability of success is the same for each trial. 4. All the trials are independent of each other.
According to the binomial formula the binomial probability of such an outcome can be calculated as follows:
$$P(k,n,p) = \frac { n! }{ (n-k)!k! } { p }^{ k }{ (1-p) }^{ n-k }.$$
A cumulative binomial probability refers to the probability that the binomial experiment outcomes fall within a specified range. Thus, the lower cumulative binomial probability is the probability of no more than \(k\) successes:
$${ P }_{ l }(k,n,p)=\sum _{ x=0 }^{ k }{ \frac { n! }{ (n-x)!x! } { p }^{ x }{ (1-p) }^{ n-x } } ,$$
and the upper cumulative binomial probability is the probability of no less than \(k\) successes:
$${ P }_{ u }(k,n,p)=\sum _{ x=k }^{ n }{ \frac { n! }{ (n-x)!x! } { p }^{ x }{ (1-p) }^{ n-x } } .$$
Example of Binomial Experiment
The quality control department conducts product testing. The probability that an item is standard is 90%. Checked 20 items. • What is the probability that exactly 5 defective items will be found? • What is the probability that no more than 5 defective items will be found?
This is a binomial experiment because it complies with the above four criteria. 1. The number of trials equals to 20. 2. Each trial has only two possible outcomes: the item is defective or not defective. 3. The probability to find defective item is 10% = 0.1 for each trial. 4. Trials are independent of each other.
So, plugging all these numbers into our Binomial Probability Calculator we can easily get the results.
• The probability that exactly 5 defective items will be found is equal to 3.2%. • To find out the probability that no more than 5 defective items will be found we have to select ‘No more than “k” successes’ option in the ‘Type of binomial probability’ drop down menu. Thus we’ll get the result: 98.9%.
Related calculators
Check out our other statistics calculators such as Binomial Coefficient Calculator or Permutations Calculator .
Share this via
Privacy overview.
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
- 2×2 System of Linear Equations Calculator
- 3×3 System of Linear Equations Calculator
- Angle Between Two Vectors Calculator
- Completing the Square Calculator
- Cross Product Calculator
- Cubic Equation Calculator
- Distance Between Two Points Calculator
- Dot Product Calculator
- Factoring Trinomials Calculator
- Matrix Calculator
- Matrix Operations Calculator
- Perfect Square Calculator
- Point Slope Form Calculator
- Quadratic Formula Calculator
- Vector Addition Calculator
- Vector Subtraction Calculator
- Alcohol Dilution Calculator
- Average Atomic Mass Calculator
- Bond Order Calculator
- Buffer pH Calculator
- Chemical Equation Balancer Calculator
- Chemical Reaction Calculator
- Degree of Unsaturation Calculator
- Dilution Calculator
- Empirical Formula Calculator
- Equilibrium Constant Calculator
- Grams to Atoms Calculator
- Half-Life Calculator
- Ionic Strength Calculator
- Mass Percent Calculator
- Mass to Mole Calculator
- Mixing Ratio Calculator
- Molality Calculator
- Molarity Calculator
- Mole Calculator
- Mole Fraction Calculator
- Molecular Formula Calculator
- Molecular Weight Calculator
- Moles to Atoms Converter
- Percent Composition Calculator
- Percent Yield Calculator
- pH Calculator
- Stoichiometry Calculator
- Theoretical Yield Calculator
- Add Time Calculator
- Average Time Calculator
- Business Days Calculator
- Chronological Age Calculator
- Day Counter Calculator
- Day of Week Calculator
- Day of Year Calculator
- Decimal to Time Calculator
- Military Time Converter
- Random Date Generator
- Random Time Generator
- Roman Numerals Date Converter
- Subtract Time Calculator
- Time to Decimal Calculator
- Week Number Calculator
- Basis Point Calculator
- CAGR Calculator
- Cap Rate Calculator
- EBIT Calculator
- EBITDA Calculator
- Gross Margin Calculator
- Internal Rate of Return Calculator
- Markup Calculator
- Net Present Value Calculator
- Percent Growth Rate Calculator
- Percent Off Calculator
- Return on Investment Calculator
- Simple Interest Calculator
- Arc Length Calculator
- Centroid Calculator
- Circle Calculator
- Cone Volume Calculator
- Cylinder Volume Calculator
- Ellipse Calculator
- Pyramid Volume Calculator
- Pythagorean Theorem Calculator
- Rhombus Area Calculator
- Right Triangle Calculator
- Sector Area Calculator
- Sphere Calculator
- Triangle Calculator
- A1C Calculator
- BAI Calculator
- Basal Metabolic Rate Calculator
- Bedtime Calculator
- Blood Alcohol Level Calculator
- Blood Sugar Converter
- BMI Calculator
- BMI Calculator for Children
- Body Fat Calculator
- BSA Calculator
- Caffeine Calculator
- Child Blood Type Calculator
- Child Height Predictor
- FFMI Calculator
- Ideal Body Weight Calculator
- Lean Body Mass Calculator
- Max Heart Rate Calculator
- Mean Arterial Pressure Calculator
- One Rep Max Calculator
- Pace Calculator
- Pregnancy Due Date Calculator
- Prostate Volume Calculator
- Sleep Calculator
- Smoking Pack Year Calculator
- Sobriety Calculator
- Standard Drinks Calculator
- Steps to Miles Calculator
- Total Body Water Calculator
- Waist to Hip Ratio Calculator
- Wilks Calculator
- Arithmetic Mean Calculator
- Arithmetic Sequence Calculator
- Binary Number Converter
- Comparing Fractions Calculator
- Complex Number Functions Calculator
- Complex Numbers Calculator
- Convolution Calculator
- Cube Root Calculator
- Decimal To Fraction Converter
- Equivalent Fractions Calculator
- Exponent Calculator
- Exponential Decay Calculator
- Factorial Calculator
- Factoring Calculator
- Fibonacci Calculator
- Fraction Exponent Calculator
- Fraction To Decimal Converter
- Geometric Mean Calculator
- Geometric Sequence Calculator
- Golden Ratio Calculator
- Greatest Common Divisor Calculator
- Harmonic Mean Calculator
- Hyperbolic Functions Calculator
- Least Common Denominator Calculator
- Least Common Multiple Calculator
- Linear Interpolation Calculator
- Midpoint Calculator
- Mixed Fractions Calculator
- Modulo Calculator
- Parallel Line Calculator
- Perpendicular Line Calculator
- Polar Coordinates Calculator
- Prime Factorization Calculator
- Proportion Calculator
- Reciprocal Calculator
- Remainder Calculator
- Roman Numerals Calculator
- Rounding Calculator
- Simplify Fraction Calculator
- Simplifying Radical Expressions Calculator
- Sum of Squares Calculator
- Trigonometric Functions Calculator
- Weighted Average Calculator
- Average of Percentages Calculator
- Decimal to Percent Calculator
- Fraction to Percent Calculator
- Percent Error Calculator
- Percent to Decimal Calculator
- Percent to Fraction Calculator
- Percentage Calculator
- Percentage Difference Calculator
- Percentage Increase Calculator
- Percentage of a Percentage Calculator
- Acceleration Calculator
- Boyle’s Law Calculator
- Capacitance Calculator
- Capacitive Reactance Calculator
- Capacitor Energy Calculator
- Capacitors in Series Calculator
- Center of Mass Calculator
- Centripetal Force Calculator
- Charles’ Law Calculator
- Coulomb’s Law Calculator
- Electric Potential Calculator
- Gay-Lussac’s Law Calculator
- Gravitational Force Calculator
- Hooke’s Law Calculator
- Ideal Gas Law Calculator
- Inductive Reactance Calculator
- Inductors in Parallel Calculator
- Inductors in Series Calculator
- Kepler’s Third Law Calculator
- Kinetic Energy Calculator
- Moment of Inertia Calculator
- Momentum Calculator
- Ohm’s Law Calculator
- Parallel Capacitor Calculator
- Parallel Resistor Calculator
- Pressure Calculator
- Resonant Frequency Calculator
- Series Resistor Calculator
- Specific Heat Calculator
- Torque Calculator
- Velocity Calculator
- Voltage Divider Calculator
- Wavelength Calculator
- Work Calculator
- Average Calculator
- Bayes’ Theorem Calculator
- Benford’s Law Calculator
- Binomial Coefficient Calculator
- Birthday Paradox Calculator
- Chebyshev’s Theorem Calculator
- Chi Square Calculator
- Correlation Coefficient Calculator
- Covariance Calculator
- Empirical Rule Calculator
- Exponential Regression Calculator
- Frequency Distribution Calculator
- Hypergeometric Distribution Calculator
- Linear Regression Calculator
- Mean, Median, Mode Calculator
- Midrange Calculator
- Multinomial Distribution Calculator
- Number Sorter
- Odds To Probability Calculator
- Outlier Calculator
- P-value Calculator
- Percentile Calculator
- Percentile Rank Calculator
- Permutations Calculator
- Poisson Distribution Calculator
- Pseudo Random Number Generator
- Quadratic Regression Calculator
- Quartile Calculator
- Root Mean Square Calculator
- Standard Deviation Calculator
- Backwards Text Generator
- Line Counter
- List Randomizer
- List Sorter
- Number to Words Converter
- Random Letter Generator
- Reverse List Generator
- Text Case Converter
- Text Compare Tool
- Text Repeater
- Text Word Counter
- Tiny Text Generator
- Upside Down Text Generator
- Wide Text Generator
- Word Frequency Counter
- Word Sorter
- Words to Numbers Converter
- Area Conversion Calculator
- Centimeters to Pixels Converter
- Clothing Sizes Converter
- dBm to Watts Converter
- Length Conversion Calculator
- Mass Conversion Calculator
- Power Conversion Calculator
- PPM Calculator
- Pressure Conversion Calculator
- Radians to Degrees Conversion Calculator
- Temperature Conversion Calculator
- Time Converter
Binomial Distribution Calculator
Calculators >
Binomial distributions involve two choices — usually “success” or “fail” for an experiment. This binomial distribution calculator can help you solve bimomial problems without using tables or lengthy equations. You do need to know a couple of key items to plug into the calculator and then you’ll be set!
- Probability(P) — percentage or decimal
- Number of trials (n)
- Successes (X) — ranges are acceptable, for example an X of between 0 and 4 successes
- For the first box (p), enter the probability of success in a trial as a decimal. This may be given to you as a percentage (i.e. 80% of respondents…), or you may be given a word problem that you need to convert to a decimal (i.e. a multiple choice test with four answers would have a .25 probability of a right answer each time you guessed).
- In the second box, enter the number of trials (n).
- The next two boxes, X1 and X2, allow you to enter a range, i.e. from 0 to 4 you would enter 0 in the X1 box and 4 in the X2 box. If you do not want a range, but rather an exact number, enter the number twice–once in each box (i.e. for “exactly 9” you would enter 9 in both X1 and X2).
What’s the probability of any given trial being a success? (p)
How many trials are there total? (n)
How many trials were successful? (x 1 )
How many trials were successful? (x 2 )
The probability of between and successes is .
How to find the answer
The way mortal humans do it.
If you’re like most people, using a formula over and over again to get the answers you want doesn’t sound like fun!
Most people use a binomial distribution table to look up the answer, like the one on this site . The problem with most tables, including the one here, is that it doesn’t cover all possible values of p, or n. So if you have p = .64 and n = 256, you probably won’t be able to simply look it up in a table.
The alternative method is to use a calculator like this one! Many scientific calculators like the TI-89 can find the answer to problems like these.
If you want to know how the numbers work, then read on!
The “Mathy” Way
To figure out what the total probability is, first we have to figure out the probability of each value of x , using this formula:
| p (1-p) |
So if your range is from to , you’d have to use that formula for . Then when you got the answer from each of those, you’d add them all up together to get the total:
P( … ) =
The graph below shows each possible value of x along the bottom, and the bar represents the chance that x will actually equal that value during a real experiment. Yellow bars means the value is in the range you chose, and if you look at the list above, you’ll see the bars correspond to the answers, and you’ll also see that if you added up all the yellow areas, you’d get the total from above also.
Binomial Distribution Calculator
Use this binomial probability calculator to easily calculate binomial cumulative distribution function and probability mass given the probability on a single trial, the number of trials and events. It can calculate the probability of success if the outcome is a binomial random variable, for example if flipping a coin. The calculator can also solve for the number of trials required.
Related calculators
- Using the Binomial Probability Calculator
- What is a Binomial Distribution?
- What is a Binomial Probability?
- Binomial Cumulative Distribution Function (CDF)
Using the Binomial Probability Calculator
You can use this tool to solve either for the exact probability of observing exactly x events in n trials, or the cumulative probability of observing X ≤ x , or the cumulative probabilities of observing X < x or X ≥ x or X > x. Simply enter the probability of observing an event (outcome of interest, success) on a single trial (e.g. as 0.5 or 1/2, 1/6 and so on), the number of trials and the number of events you want the probability calculated for. As long as the procedure generating the event conforms to the random variable model under a Binomial distribution the calculator applies. In other words, X must be a random variable generated by a process which results in Binomially-distributed, Independent and Identically Distributed outcomes (BiIID). For example, you can compute the probability of observing exactly 5 heads from 10 coin tosses of a fair coin (24.61%) , of rolling more than 2 sixes in a series of 20 dice rolls (67.13%) and so on. See more examples below.
Under the same conditions you can use the binomial probability distribution calculator above to compute the number of attempts you would need to see x or more outcomes of interest (successes, events). For example, if you know you have a 1% chance (1 in 100) to get a prize on each draw of a lottery, you can compute how many draws you need to participate in to be 99.99% certain you win at least 1 prize ( 917 draws ). Note that this example doesn't apply if you are buying tickets for a single lottery draw (the events are not independent).
Sequences of Bernoulli trials: trials in which the outcome is either 1 or 0 with the same probability on each trial result in and are modelled as binomial distribution so any such problem is one which can be solved using the above tool: it essentially doubles as a coin flip calculator .
What is a Binomial Distribution?
The binomial distribution X~Bin(n,p) is a probability distribution which results from the number of events in a sequence of n independent experiments with a binary / Boolean outcome: true or false, yes or no, event or no event, success or failure. These are also known as Bernoulli trials and thus a Binomial distribution is the result of a sequence of Bernoulli trials. The parameters which describe it are n - number of independent experiments and p the probability of an event of interest in a single experiment. It is often used as a teaching device and the practical applications of probability theory and statistics due its many desirable properties such as a known standard deviation and easy to compute cumulative distribution function and inverse function.
The binomial probability distribution can be used to model the number of events in a sample of size n drawn with replacement from a population of size N, e.g. coin tosses, dice rolls, and so on. If the sampling is carried out without replacement they are no longer independent and the result is a hypergeometric distribution, although the binomial remains a decent approximation if N >> n.

The above is a randomly generated binomial distribution from 10,000 simulated binomial experiments, each with 10 Bernoulli trials with probability of observing an event of 0.2 (20%).
What is a Binomial Probability?
A probability for a certain outcome from a binomial distribution is what is usually referred to as a "binomial probability". It can be calculated using the formula for the binomial probability distribution function (PDF), a.k.a. probability mass function (PMF): f(x) , as follows:

Note that the above equation is for the probability of observing exactly the specified outcome. However, often when searching for a binomial probability formula calculator people are actually looking to calculate the cumulative probability of a binomially-distributed random variable: the probability of observing x or less than x events (successes, outcomes of interest).
Binomial Cumulative Distribution Function (CDF)
The cumulative distribution function (CDF) of the Binomial distribution is what is needed when you need to compute the probability of observing less than or more than a certain number of events/outcomes/successes from a number of trials. The Binomial CDF formula is simple:

Therefore, the cumulative binomial probability is simply the sum of the probabilities for all events from 0 to x. Our binomial distribution calculator uses the formula above to calculate the cumulative probability of events less than or equal to x, less than x, greater than or equal to x and greater than x for you. These are all cumulative binomial probabilities.
The inverse function is required when computing the number of trials required to observe a certain number of events, or more, with a certain probability. For this we use the inverse normal distribution function which provides a good enough approximation.
Examples
Example 1: Coin flipping. If a fair coin (p = 1/2 = 0.5) is tossed 100 times, what is the probability of observing exactly 50 heads? What is the probability of observing more than 50 heads? Entering 0.5 or 1/2 in the calculator and 100 for the number of trials and 50 for "Number of events" we get that the chance of seeing exactly 50 heads is just under 8% while the probability of observing more than 50 is a whopping 46%. While in an infinite number of coin flips a fair coin will tend to come up heads exactly 50% of the time, in any small number of flips it is highly unlikely to observe exactly 50% heads.
Example 2: Dice rolling. If a fair dice is thrown 10 times, what is the probability of throwing at least one six? We know that a dice has six sides so the probability of success in a single throw is 1/6. Thus, using n=10 and x=1 we can compute using the Binomial CDF that the chance of throwing at least one six (X ≥ 1) is 0.8385 or 83.85 percent.
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Binomial Distribution Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/binomial-probability-calculator.php URL [Accessed Date: 09 Sep, 2024].
The author of this tool

Statistical calculators
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Binomial Distribution: Uses & Calculator
By Jim Frost 2 Comments
What is the Binomial Distribution?
The binomial distribution is a discrete probability distribution that calculates the likelihood an event will occur a specific number of times in a set number of opportunities. Use this distribution when you have a binomial random variable. These variables count how often an event occurs within a fixed number of trials. They have only two possible outcomes that are mutually exclusive.
For example, the binomial probability distribution can answer the following questions. What is the probability of getting:
- Six heads when you toss the coin ten times?
- 12 women in a sample size of 20?
- Three defective items in a batch of 100?
- Two flu infections over 20 years?
This distribution is an example of a Probability Mass Function (PMF) because it calculates likelihoods for discrete random variables. It is an extension of the Bernoulli distribution that can model only 1 trial.
In this post, learn how to use the binomial distribution, its cumulative form, and when you can use it. I also include a binomial calculator that you can use with what you learn.
Note that this post focuses on how to use and graph the binomial distribution. If you want to learn how to calculate the probabilities by hand, please read Binomial Distribution Formula: Probability, Standard Deviation & Mean .
Binomial Probabilities

I’ll start by using statistical software to calculate the binomial probabilities and create distribution plots. This process will help you understand what you can learn from it.
Suppose you’re playing a game where rolling sixes on a die is really good. You want to know the probability of rolling exactly three sixes in ten die rolls. In this example, the number of events is 3 (X), the number of trials is 10 (N), and the probability (p) is 1/6 = 0.1667.
My software tells me that the likelihood is:

The binomial probability distribution calculates a likelihood of 0.155095 for rolling precisely three sixes in ten rolls.
That’s interesting but perhaps not so helpful by itself. We’re also interested in the chances for rolling other numbers of sixes. Seeing the distribution of probabilities for different numbers of sixes is much more helpful.
Binomial Distribution Graph
The binomial distribution graph is useful because it displays the probability of differing numbers of successes (Xs) out of the total number of trials (N). In the graph below, the distribution plot finds the likelihood of rolling exactly no sixes, 1 six, 2 sixes, 3 sixes, . . ., and up to 10 sixes in the ten die rolls. Using this approach, the binomial distribution graph covers the complete range of possible successes up to the total number of trials.
I like these graphs because they emphasize how we’re working with a distribution, and it’s easy to see which values happen more frequently.
In the chart, each bar represents the probability of rolling a specific number of sixes out of ten die rolls. The graph does not show the chances for seven and higher because the likelihoods of that many sixes in just ten rolls are too low to display on the chart.

The binomial distribution graph indicates the probability of rolling no sixes is about 16%. The highest chance is rolling one six (32%). Although, rolling two sixes occurs almost as frequently. Probabilities drop off quickly starting with three sixes. Additionally, the bar for three sixes matches our earlier result of 0.155095.
Related post : Understanding Probability Distributions
Binomial Cumulative Distribution Function
The binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (X) within a certain number of trials (N). However, many times you’re not interested in just one specific value for a binomial random variable. For example, in the die rolling example above, you might know from experience that rolling three or more sixes within ten rolls means you’re doing well. So, you actually want to learn the probability of rolling at least three sixes.
Let me introduce you to the binomial cumulative distribution function.
Technically, the binomial cumulative probability calculates the likelihood of obtaining less than or equal to X events in N trials. If you need to obtain a ≥ probability, use the inverse cumulative distribution. These days, statistical software will generally let you specify the direction of the cumulative function for the binomial distribution from the start. I’ll use the binomial distribution graph again to show you how it works.
For our example, we want to know the chances of rolling ≥ 3 sixes in 10 rolls. Below, the shaded region shows the inverse cumulative probability of rolling at least three sixes in ten die rolls.

The likelihood for rolling three or more sixes in ten rolls is 0.2249, not quite 1 in 4.
For a real-world example, see how I’ve used the binomial distribution to model the number of flu infections (X) for the vaccinated vs. unvaccinated over 20 years (N).
Learn more about Cumulative Distribution Functions: Uses, Graphs & vs PDF .
Binomial Distribution Assumptions and Notation
The binomial distribution models the probabilities for a binomial random variable having exactly X successes occurring in N trials. Your variable must satisfy the following requirements to be a binomial random variable. The binomial distribution is appropriate only for data that fulfill these assumptions.
- There must be only two possible outcomes per trial . For example, defective or not defective, sale or no sale, pass or fail, etc.
- The trials are independent . One trial’s outcome does not affect the subsequent trial. For instance, one coin toss doesn’t affect the result of the following coin toss. Learn more about Independent Events .
- The probability remains constant over time . In some areas, this assumption is true due to the physical characteristics of the process, such as coin tosses and die rolls. However, the probability won’t necessarily remain constant in other contexts. For example, the likelihood that a manufacturing process creates defective parts can change over time. If the probability can change, use the P chart ( a control chart ) to confirm this assumption.
Bernoulli Trials
Typically, you’ll use the binomial distribution when you have Bernoulli Trials, also known as Binomial Experiments. These trials involve binomial random variables that satisfactorily follow the assumptions above. In these trials, analysts label one of the possible outcomes as a success and the other outcome a failure.
A Bernoulli trial contains a set number of trials where the probability of a success is constant. The experiment counts the number of successes (X) out of the total number of trials (N).
You can think of the binomial probability distribution as modeling the number of successes (X) in a sample size of N.
Parameters and Notation
The binomial distribution has two parameters , n and p.
- n : the number of trials.
- p : the event or success probability.
You denote a binomial distribution as b(n,p).
Alternatively, you can write X∼b(n,p), which means that your binomial random variable X follows a binomial probability distribution with n trials and an event probability of p.
The previous examples assess probabilities corresponding with rolling sixes in a series of 10 die rolls. In this scenario, success is rolling a six, while a failure is rolling anything other than a six. The probability of rolling a six is 1/6 = 0.1667.
If rolling sixes is our random variable X, and we roll the die ten times, we can use the following notation for the binomial distribution:
X∼b(10,0.1667)
Binomial Distribution Calculator
Use this binomial distribution calculator to calculate the binomial probabilities and cumulative probabilities. Note that it uses “events” to indicate the number of trials (n).
Next, change exactly r successes to r or more successes . The calculator displays 22.487, matching the results for our example with the binomial inverse cumulative distribution.
Now, try one yourself. Imagine you’re drawing a random sample of 20 from a population where 10% are statisticians. You’re hoping that your study will have 3 or fewer statisticians because they’ll gang up and ask too many pesky questions about your study design. What is the likelihood of obtaining ≤ 3 statisticians?
See the correct answer at the end of this post.
Finally, the binomial and beta distributions are closely related. Click the link to learn more!
For more information about how to use binary data, read my posts, Maximize the Value of Your Binary Data , the Negative Binomial Distribution , the Geometric Distribution , and the Hypergeometric Distribution .
In the calculator example, there is an 86.7% chance of having ≤ 3 statisticians in your sample of 20 people.
Share this:

Reader Interactions
August 25, 2022 at 9:55 pm
Is there some way to combine binomial distributions? Here’s an example. Ann, Bob, and Carol are shooting threes on a basketball court. Ann takes 50 shots and has a 30% success rate. Bob takes 30 shots and has a 20% success rate. Carol takes 20 shots and has a 10% success rate. I can use the cumulative binomial distribution to calculate the chance that Ann makes 10 or more shots or that Bob makes 10 or more shots. How do I calculate the probability that the three of them combine to make 20 or more shots?
August 25, 2022 at 6:45 pm
Would binomial distributions be suitable for determining the probability of a prisoner re-offending once released from prison? Thank you.
Comments and Questions Cancel reply
Calculator: Binomial Probability
Binomial Probability Calculator
This calculator will compute the probability of an individual binomial outcome (i.e., a binomial probability), given the number of successes, the number of trials, and the probability of a successful outcome occurring. Please enter the necessary parameter values, and then click 'Calculate'.
| Successes: | ||
| Trials: |
Binomial Distribution Calculator
| Probability of success (single trial) | p | |
| Number of trials | n | |
| Number of successes | x | |
| Cumulative probability | ||
| Cumulative probability | ||
| Cumulative probability | ||
| Cumulative probability | ||
| N choose X | C | |
| Mean | μ | |
| Variance | σ | |
| Standard Deviation | σ |
Binomial Distributions
A binomial experiment with n trials, probability of success p , and x successes, has Binomial Probability: $$P(X = x) = _nC_x * p^x * (1 - p)^{n - x}$$ Where "n choose x" is: $$(_nC_x) = \frac{n!}{x! (n - x)!}$$ Mean: $$ \mu = n * p$$ Variance: $$ \sigma = n * p * (1-p)$$ Standard Deviation: $$ \sigma^2 = \sqrt{n * p * (1-p)}$$
Requirements
Binomial Experiments must have:
- Trials with 2 outcomes (success or failure)
- Independent trials (the probability of a particular outcome is constant)
p must be between 0 and 1, n and x must be positive integers where n ≥ x
Learn more on Wikipedia and Math is Fun , or watch a 3Blue1Brown video .
Made with Google Charts , MathJax , SvelteKit ,

- Calculators
- Descriptive Statistics
- Merchandise
- Which Statistics Test?
Binomial Test Calculator
This binomial test calculator determines the probability of a particular outcome (K) across a certain number of trials ( n ), where there are precisely two possible outcomes.
To use the calculator, enter the values of n , K and p into the table below ( q will be calculated automatically), where n is the number of trials or observations, K is number of occasions the actual (or stipulated) outcome occurred, and p is the probability the outcome will occur on any particular occasion.
Things to remember: (a) the binomial test is appropriate only when you've got just two possible outcomes (or categories, etc.); (b) n and K will be frequencies; and (c) the value for p will fall somewhere between 0 and 1 - it's a proportion.
| K | |||
| not calculated |

Binomial Distribution Calculator
binomial distribution calculator - to estimate the probability of number of success or failure in a sequence of n independent trials or experiments. The success or failure experiment which is used in this calculator is also called as Bernoulli 's experiment or distribution or trial and is the fundamental for the binomial test of statistical significance. In probability & statistics for data analysis, binomial distribution is a discrete probability function widely used method to model the number of successes and failures in n independent numbers of trials or experiments. P(x) is the probability of x successes occur in the n number of events, p is the probability of success and q is the probability of failure often denoted by q = (1 - p) . The binomial distribution arise for the following 4 conditions, when the event has 1. n identical trials or experiments 2. Two possible outcomes for each trial or experiments are success and failure. 3. Each trials or experiments are independent, e.g. each coin toss doesn't affect the others. 4. P(success) = p is the probability of success same for each trial or experiments.
- Personality
Binomial Calculator
This binomial calculator can help you calculate individual and cumulative binomial probabilities of an experiment considering the probability of success on a single trial, no. of trials and no. of successes. You can learn more below the form.
Other Tools You May Find Useful
■ Correlation Coefficient Calculator
■ Sample Size Calculator
■ Poisson Distribution Calculator
■ Chi Square Calculator
How does this binomial calculator work?
This is a statistics tool designed to help you compute individual and cumulative binomial probabilities for an experiment having the following particularities:
■ The experiment requires repeated trials while each trial can have one of the two potential outcomes: either success or failure.
■ The probability associated with the occurrence of a particular outcome on any given trial is constant.
■ The trials are independent.
The algorithm behind this binomial calculator is based on the formulas provided below:
1) B(s=s given; n, p) = { n! / [ s! (n - s)! ] } * P s * (1 - P) n – s
2) B(s<s given; n, p) is the sum of probabilities obtained for all cases from (s=0) to (s given – 1).
3) B(s≤s given; n, p) is the sum of probabilities that results for all cases from (s=0) to (s given).
4) B(s>s given; n, p) = 1 - B(s≤s given; n, p)
5) B(s≥s given; n, p) = B(s=s given; n, p) + B(s>s given; n, p)
P = Probability of success on a single trial
n = Number of trials
s = Number of successes
What is a binomial probability?
The binomial probability represents the probability of getting an exact number of successes (s) in a given number of trials (n) within an experiment.
What is the cumulative binomial probability?
The cumulative binomial probability is obtained by adding up the individual probabilities of getting each number of successes within a specified range.
For instance the cumulative probability of extracting less than or equal 2 (s) white balls out of 6 (n) is equivalent to:
[the probability of extracting exactly 0 (s=0) white balls out of the 6] + [the probability of getting exactly 1 (s=1) ball in white out of 6] + [the probability of extracting exactly 2 (s=2) white balls]
Teach yourself statistics
Binomial Probability Distribution
To understand binomial distributions and binomial probability, it helps to understand binomial experiments and some associated notation; so we cover those topics first.
Note: Your browser does not support HTML5 video. If you view this web page on a different browser (e.g., a recent version of Edge, Chrome, Firefox, or Opera), you can watch a video treatment of this lesson.
Binomial Experiment
A binomial experiment is a statistical experiment that has the following properties:
- The experiment consists of n repeated trials.
- Each trial can result in just two possible outcomes. We call one of these outcomes a success and the other, a failure.
- The probability of success, denoted by P , is the same on every trial.
- The trials are independent ; that is, the outcome on one trial does not affect the outcome on other trials.
Consider the following statistical experiment. You flip a coin 2 times and count the number of times the coin lands on heads. This is a binomial experiment because:
- The experiment consists of repeated trials. We flip a coin 2 times.
- Each trial can result in just two possible outcomes - heads or tails.
- The probability of success is constant - 0.5 on every trial.
- The trials are independent; that is, getting heads on one trial does not affect whether we get heads on other trials.
The following notation is helpful, when we talk about binomial probability.
- x : The number of successes that result from the binomial experiment.
- n : The number of trials in the binomial experiment.
- P : The probability of success on an individual trial.
- Q : The probability of failure on an individual trial. (This is equal to 1 - P .)
- n! : The factorial of n (also known as n factorial).
- b( x ; n, P ): Binomial probability - the probability that an n -trial binomial experiment results in exactly x successes, when the probability of success on an individual trial is P .
- n C r : The number of combinations of n things, taken r at a time.
Binomial Distribution
A binomial random variable is the number of successes x in n repeated trials of a binomial experiment. The probability distribution of a binomial random variable is called a binomial distribution .
Suppose we flip a coin two times and count the number of heads (successes). The binomial random variable is the number of heads, which can take on values of 0, 1, or 2. The binomial distribution is presented below.
| Number of heads | Probability |
|---|---|
| 0 | 0.25 |
| 1 | 0.50 |
| 2 | 0.25 |
The binomial distribution has the following properties:
- The mean of the distribution (μ x ) is equal to n * P .
- The variance (σ 2 x ) is n * P * ( 1 - P ).
- The standard deviation (σ x ) is sqrt[ n * P * ( 1 - P ) ].
Binomial Formula and Binomial Probability
The binomial probability refers to the probability that a binomial experiment results in exactly x successes. For example, in the above table, we see that the binomial probability of getting exactly one head in two coin flips is 0.50.
Given x , n , and P , we can compute the binomial probability based on the binomial formula:
Binomial Formula. Suppose a binomial experiment consists of n trials and results in x successes. If the probability of success on an individual trial is P , then the binomial probability is:
b( x ; n, P ) = n C x * P x * (1 - P) n - x or b( x ; n, P ) = { n! / [ x! (n - x)! ] } * P x * (1 - P) n - x
Example 1 Suppose a die is tossed 5 times. What is the probability of getting exactly 2 fours?
Solution: This is a binomial experiment in which the number of trials is equal to 5, the number of successes is equal to 2, and the probability of success on a single trial is 1/6 or about 0.167. Therefore, the binomial probability is:
b(2; 5, 0.167) = 5 C 2 * (0.167) 2 * (0.833) 3 b(2; 5, 0.167) = 10 * (0.167) 2 * (0.833) 3 b(2; 5, 0.167) = 0.161
Example 2 What is the probability that the world series will last 4 games? 5 games? 6 games? 7 games? Assume that the teams are evenly matched.
Solution: The solution to this problem requires a creative application of the binomial formula. If you can follow the logic of this solution, you have a good understanding of the material covered in the tutorial, to this point.
In the world series, there are two baseball teams. The series ends when the winning team wins 4 games. Therefore, we define a success as a win by the team that ultimately becomes the world series champion.
For the purpose of this analysis, we assume that the teams are evenly matched. Therefore, the probability that a particular team wins a particular game is 0.5.
Let's look first at the simplest case. What is the probability that the series lasts only 4 games. This can occur if one team wins the first 4 games. The probability of the National League team winning 4 games in a row is:
b(4; 4, 0.5) = 4 C 4 * (0.5) 4 * (0.5) 0 = 0.0625
Similarly, when we compute the probability of the American League team winning 4 games in a row, we find that it is also 0.0625. Therefore, probability that the series ends in four games would be 0.0625 + 0.0625 = 0.125; since the series would end if either the American or National League team won 4 games in a row.
Now let's tackle the question of finding probability that the world series ends in 5 games. The trick in finding this solution is to recognize that the series can only end in 5 games, if one team has won 3 out of the first 4 games. So let's first find the probability that the American League team wins exactly 3 of the first 4 games.
b(3; 4, 0.5) = 4 C 3 * (0.5) 3 * (0.5) 1 = 0.25
Okay, here comes some more tricky stuff, so listen up. Given that the American League team has won 3 of the first 4 games, the American League team has a 50/50 chance of winning the fifth game to end the series. Therefore, the probability of the American League team winning the series in 5 games is 0.25 * 0.50 = 0.125. Since the National League team could also win the series in 5 games, the probability that the series ends in 5 games would be 0.125 + 0.125 = 0.25.
The rest of the problem would be solved in the same way. You should find that the probability of the series ending in 6 games is 0.3125; and the probability of the series ending in 7 games is also 0.3125.
Cumulative Binomial Probability
A cumulative binomial probability refers to the probability that the binomial random variable falls within a specified range (e.g., is greater than or equal to a stated lower limit and less than or equal to a stated upper limit).
To compute a cumulative binomial probability, we find the sum of relevant individual binomial probabilities, as illustrated in the examples below.
Example 3 The probability that a student is accepted to a prestigious college is 0.3. If 5 students from the same school apply, what is the probability that at most 2 are accepted?
Solution: To solve this problem, we compute 3 individual probabilities, using the binomial formula. The sum of all these probabilities is the answer we seek. Thus,
b(x < 2; 5, 0.3) = b(x = 0; 5, 0.3) + b(x = 1; 5, 0.3) + b(x = 2; 5, 0.3) b(x < 2; 5, 0.3) = 0.1681 + 0.3601 + 0.3087 b(x < 2; 5, 0.3) = 0.8369
Example 4 What is the probability of obtaining 45 or fewer heads in 100 tosses of a coin?
Solution: To solve this problem, we compute 46 individual binomial probabilities, using the binomial formula. The sum of all these binomial probabilities is the answer we seek. Thus,
b(x < 45; 100, 0.5) = b(x = 0; 100, 0.5) + b(x = 1; 100, 0.5) + . . . + b(x = 44; 100, 0.5) + b(x = 45; 100, 0.5) b(x < 45; 100, 0.5) = 0.184
Binomial Calculator
As you may have noticed, the binomial formula requires many time-consuming computations. The Binomial Calculator can do this work for you - quickly, easily, and error-free. Use the Binomial Calculator to compute binomial probabilities and cumulative binomial probabilities. The calculator is free. It can found in the Stat Trek main menu under the Stat Tools tab. Or you can tap the button below.
Here is the solution to this problem, using the Binomial Calculator :
Example 5 Suppose it were possible to take a simple random sample of 120 newborns. Find the probability that no more than 40% will be boys. Assume equal probabilities for the births of boys and girls.
Solution: We know that 40% of 120 is 48. Therefore, we want to know the probability that a random sample of 120 newborns will include no more than 48 boys. The solution to this problem requires that we compute the following cumulative binomial probability.
b(x < 48; 120, 0.5) = b(x = 0; 120, 0.5) + b(x = 1; 120, 0.5) + ... + b(x = 48; 120, 0.5) b(x < 48; 120, 0.5) = 0.0 + 0.0 + ... + 0.00662 b(x < 48; 120, 0.5) = 0.01766
Note: Finding this cumulative binomial probability requires requires computing 49 individual binomial probabilities. It can be done by hand, but it is much easier to use the Binomial Calculator , as shown below:

IMAGES
VIDEO
COMMENTS
Binomial Distribution Probability Calculator
Binomial Distribution Calculator
Binomial Probability Calculator
Let's run these values through our calculator: Input Values: Enter 10 for the number of trials (n), 5 for the number of successful outcomes (x), and 0.5 for the probability of success (p). Review: The calculator promptly computes the binomial probability, providing the likelihood of getting exactly 5 heads in 10 flips.
A binomial probability calculator can be a useful tool for calculating the probabilities of various outcomes in binomial experiments, enabling us to make informed decisions in real-world applications of statistics. Binomial Distribution Basics Probability Distribution. The binomial distribution is a discrete probability distribution used to ...
In statistics, the binomial distribution is a discrete probability distribution that only gives two possible results in an experiment either failure or success. For example, if we toss with a coin, there can only be two possible outcomes: tails or heads, and when taking any test, there can only be two outcomes: pass or fail.
Enter the values in binomial probability distribution calculator to compute probabilities in scenarios involving a fixed number of independent trials, each with two possible outcomes: success or failure. Binomial Probability Distribution Calculator n (trials) p (probability) k (successes) P(X = k) P(X ≤ k) 10 0.5 5 0.2461 0.6230 20 0.3 6 0.2066 0.8670 15...
In statistics, a binomial distribution is a probability distribution of the number of successes in a sequence of independent experiments or trials. The result of each experiment must be dichotomous, which means the result must be a yes/no, success/fail, heads/tails, true/false, or similar outcome. Unlike a normal distribution, a binomial ...
Use the binomial model to find the probability that 2 out 5 members of the Dawson family get the flu this year. DIRECTIONS: Enter the 5 trials, 0.15 probability of success in parentheses. Set the min and max = 2 for the number of favorable outcomes. to save your graphs! Explore math with our beautiful, free online graphing calculator.
Binomial distribution formula. The binomial probability refers to the probability that a binomial experiment of \(n\) trials results in exactly \(k\) successes given each independent trial has the probability \(p\).. The binomial experiment (or Bernoulli experiment) is a statistical experiment that has the following four properties:. 1. Fixed number of trials.
This binomial distribution calculator can help you solve bimomial problems without using tables or lengthy equations. You do need to know a couple of key items to plug into the calculator and then you'll be set! Probability (P) — percentage or decimal. Number of trials (n) Successes (X) — ranges are acceptable, for example an X of between ...
Using the binomial probability calculator, and plugging in the values N = 500, p = 0.05, x = 49, we will see that the probability is almost 0. So unless, you increase the probability of each sale up from 5%, you will never meet your boss's target. You can also try to reverse analyse the situation by figuring out what probability of each sale ...
Binomial Distribution Calculator
Binomial Calculator. Distributional calculator inputs; n: p: P (≤X≤ ) = : P (X ) = (X
Binomial Distribution: Uses & Calculator
This calculator will compute the probability of an individual binomial outcome (i.e., a binomial probability), given the number of successes, the number of trials, and the probability of a successful outcome occurring. Please enter the necessary parameter values, and then click 'Calculate'. The Free Statistics Calculators index now contains 106 ...
Requirements. Binomial Experiments must have: Trials with 2 outcomes (success or failure); Independent trials (the probability of a particular outcome is constant); p must be between 0 and 1, n and x must be positive integers where n ≥ x
Binomial Distribution Calculator
This binomial test calculator determines the probability of a particular outcome (K) across a certain number of trials (n), where there are precisely two possible outcomes.To use the calculator, enter the values of n, K and p into the table below (q will be calculated automatically), where n is the number of trials or observations, K is number of occasions the actual (or stipulated) outcome ...
The success or failure experiment which is used in this calculator is also called as Bernoulli's experiment or distribution or trial and is the fundamental for the binomial test of statistical significance. In probability & statistics for data analysis, binomial distribution is a discrete probability function widely used method to model the ...
The Binomial distribution is one of the most commonly used distributions in statistics. To find probabilities related to the Binomial distribution, simply fill in the values below and then click the "Calculate" button. p (probability of success on a given trial) n (number of trials) k (number of successes) P (X= 43) = 0.03007. P (X<43) = 0. ...
How does this binomial calculator work? This is a statistics tool designed to help you compute individual and cumulative binomial probabilities for an experiment having the following particularities: The experiment requires repeated trials while each trial can have one of the two potential outcomes: either success or failure.
Binomial Distribution