galvanic cell experiment errors

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 11 November 2022

Error, reproducibility and uncertainty in experiments for electrochemical energy technologies

• Graham Smith   ORCID: orcid.org/0000-0003-0713-2893 1 &
• Edmund J. F. Dickinson   ORCID: orcid.org/0000-0003-2137-3327 1  

Nature Communications volume  13 , Article number:  6832 ( 2022 ) Cite this article

11k Accesses

9 Citations

21 Altmetric

Metrics details

• Electrocatalysis
• Electrochemistry
• Materials for energy and catalysis

The authors provide a metrology-led perspective on best practice for the electrochemical characterisation of materials for electrochemical energy technologies. Such electrochemical experiments are highly sensitive, and their results are, in practice, often of uncertain quality and challenging to reproduce quantitatively.

A critical aspect of research on electrochemical energy devices, such as batteries, fuel cells and electrolysers, is the evaluation of new materials, components, or processes in electrochemical cells, either ex situ, in situ or in operation. For such experiments, rigorous experimental control and standardised methods are required to achieve reproducibility, even on standard or idealised systems such as single crystal platinum 1 . Data reported for novel materials often exhibit high (or unstated) uncertainty and often prove challenging to reproduce quantitatively. This situation is exacerbated by a lack of formally standardised methods, and practitioners with less formal training in electrochemistry being unaware of best practices. This limits trust in published metrics, with discussions on novel electrochemical systems frequently focusing on a single series of experiments performed by one researcher in one laboratory, comparing the relative performance of the novel material against a claimed state-of-the-art.

Much has been written about the broader reproducibility/replication crisis 2 and those reading the electrochemical literature will be familiar with weakly underpinned claims of “outstanding” performance, while being aware that comparisons may be invalidated by measurement errors introduced by experimental procedures which violate best practice; such issues frequently mar otherwise exciting science in this area. The degree of concern over the quality of reported results is evidenced by the recent decision of several journals to publish explicit experimental best practices 3 , 4 , 5 , reporting guidelines or checklists 6 , 7 , 8 , 9 , 10 and commentary 11 , 12 , 13 aiming to improve the situation, including for parallel theoretical work 14 .

We write as two electrochemists who, working in a national metrology institute, have enjoyed recent exposure to metrology: the science of measurement. Metrology provides the vocabulary 15 and mathematical tools 16 to express confidence in measurements and the comparisons made between them. Metrological systems and frameworks for quantification underpin consistency and assurance in all measurement fields and formal metrology is an everyday consideration for practical and academic work in fields where accurate measurements are crucial; we have found it a useful framework within which to evaluate our own electrochemical work. Here, rather than pen another best practice guide, we aim, with focus on three-electrode electrochemical measurements for energy material characterisation, to summarise some advice that we hope helps those performing electrochemical experiments to:

avoid mistakes and minimise error

report in a manner that facilitates reproducibility

consider and quantify uncertainty

Minimising mistakes and error

Metrology dispenses with nebulous concepts such as performance and instead requires scientists to define a specific measurand (“the quantity intended to be measured”) along with a measurement model ( ”the mathematical relation among all quantities known to be involved in a measurement”), which converts the experimental indicators into the measurand 15 . Error is the difference between the reported value of this measurand and its unknowable true value. (Note this is not the formal definition, and the formal concepts of error and true value are not fully compatible with measurement concepts discussed in this article, but we retain it here—as is common in metrology tuition delivered by national metrology institutes—for pedagogical purposes 15 ).

Mistakes (or gross errors) are those things which prevent measurements from working as intended. In electrochemistry the primary experimental indicator is often current or voltage, while the measurand might be something simple, like device voltage for a given current density, or more complex, like a catalyst’s turnover frequency. Both of these are examples of ‘method-defined measurands’, where the results need to be defined in reference to the method of measurement 17 , 18 (for example, to take account of operating conditions). Robust experimental design and execution are vital to understand, quantify and minimise sources of error, and to prevent mistakes.

Contemporary electrochemical instrumentation can routinely offer a current resolution and accuracy on the order of femtoamps; however, one electron looks much like another to a potentiostat. Consequently, the practical limit on measurements of current is the scientist’s ability to unambiguously determine what causes the observed current. Crucially, they must exclude interfering processes such as modified/poisoned catalyst sites or competing reactions due to impurities.

As electrolytes are conventionally in enormous excess compared to the active heterogeneous interface, electrolyte purity requirements are very high. Note, for example, that a perfectly smooth 1 cm 2 polycrystalline platinum electrode has on the order of 2 nmol of atoms exposed to the electrolyte, so that irreversibly adsorbing impurities present at the part per billion level (nmol mol −1 ) in the electrolyte may substantially alter the surface of the electrode. Sources of impurities at such low concentration are innumerable and must be carefully considered for each experiment; impurity origins for kinetic studies in aqueous solution have been considered broadly in the historical literature, alongside a review of standard mitigation methods 19 . Most commercial electrolytes contain impurities and the specific ‘grade’ chosen may have a large effect; for example, one study showed a three-fold decrease in the specific activity of oxygen reduction catalysts when preparing electrolytes with American Chemical Society (ACS) grade acid rather than a higher purity grade 20 . Likewise, even 99.999% pure hydrogen gas, frequently used for sparging, may contain more than the 0.2 μmol mol −1 of carbon monoxide permitted for fuel cell use 21 .

The most insidious impurities are those generated in situ. The use of reference electrodes with chloride-containing filling solutions should be avoided where chloride may poison catalysts 22 or accelerate dissolution. Similarly, reactions at the counter electrode, including dissolution of the electrode itself, may result in impurities. This is sometimes overlooked when platinum counter electrodes are used to assess ‘platinum-free’ electrocatalysts, accidentally resulting in performance-enhancing contamination 23 , 24 ; a critical discussion on this topic has recently been published 25 . Other trace impurity sources include plasticisers present in cells and gaskets, or silicates from the inappropriate use of glass when working with alkaline electrolytes 26 . To mitigate sensitivity to impurities from the environment, cleaning protocols for cells and components must be robust 27 . The use of piranha solution or similarly oxidising solution followed by boiling in Type 1 water is typical when performing aqueous electrochemistry 20 . Cleaned glassware and electrodes are also routinely stored underwater to prevent recontamination from airborne impurities.

The behaviour of electronic hardware used for electrochemical experiments should be understood and considered carefully in interpreting data 28 , recognising that the built-in complexity of commercially available digital potentiostats (otherwise advantageous!) is capable of introducing measurement artefacts or ambiguity 29 , 30 . While contemporary electrochemical instrumentation may have a voltage resolution of ~1 μV, its voltage measurement uncertainty is limited by other factors, and is typically on the order of 1 mV. As passing current through an electrode changes its potential, a dedicated reference electrode is often incorporated into both ex situ and, increasingly, in situ experiments to provide a stable well defined reference. Reference electrodes are typically selected from a range of well-known standardised electrode–electrolyte interfaces at which a characteristic and kinetically rapid reversible faradaic process occurs. The choice of reference electrode should be made carefully in consideration of chemical compatibility with the measurement environment 31 , 32 , 33 , 34 . In combination with an electronic blocking resistance, the potential of the electrode should be stable and reproducible. Unfortunately, deviation from the ideal behaviour frequently occurs. While this can often be overlooked when comparing results from identical cells, more attention is required when reporting values for comparison.

In all cases where conversion between different electrolyte–reference electrode systems is required, junction potentials should be considered. These arise whenever there are different chemical conditions in the electrolyte at the working electrode and reference electrode interfaces. Outside highly dilute solutions, or where there are large activity differences for a reactant/product of the electrode reaction (e.g. pH for hydrogen reactions), liquid junction potentials for conventional aqueous ions have been estimated in the range <50 mV 33 . Such a deviation may nonetheless be significant when onset potentials or activities at specific potentials are being reported. The measured potential difference between the working and reference electrode also depends strongly on the geometry of the cell, so cell design is critical. Fig.  1 shows the influence of cell design on potential profiles. Ideally the reference electrode should therefore be placed close to the working electrode (noting that macroscopic electrodes may have inhomogeneous potentials). To minimise shielding of the electric field between counter and working electrode and interruption of mass transport processes, a thin Luggin-Haber capillary is often used and a small separation maintained. Understanding of shielding and edge effects is vital when reference electrodes are introduced in situ. This is especially applicable for analysis of energy devices for which constraints on cell design, due to the need to minimise electrolyte resistance and seal the cell, preclude optimal reference electrode positioning 32 , 35 , 36 .

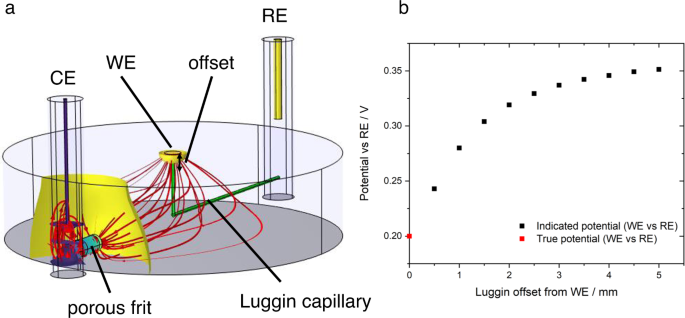
a Illustration (simulated data) of primary (resistive) current and potential distribution in a typical three-electrode cell. The main compartment is cylindrical (4 cm diameter, 1 cm height), filled with electrolyte with conductivity 1.28 S m −1 (0.1 M KCl(aq)). The working electrode (WE) is a 2 mm diameter disc drawing 1 mA (≈ 32 mA cm −2 ) from a faradaic process with infinitely fast kinetics and redox potential 0.2 V vs the reference electrode (RE). The counter electrode (CE) is connected to the main compartment by a porous frit; the RE is connected by a Luggin capillary (green cylinders) whose tip position is offset from the WE by a variable distance. Red lines indicate prevailing current paths; coloured surfaces indicate isopotential contours normal to the current density. b Plot of indicated WE vs RE potential (simulated data). As the Luggin tip is moved away from the WE surface, ohmic losses due to the WE-CE current distribution lead to variation in the indicated WE-RE potential. Appreciable error may arise on an offset length scale comparable to the WE radius.

Quantitative statements about fundamental electrochemical processes based on measured values of current and voltage inevitably rely on models of the system. Such models have assumptions that may be routinely overlooked when following experimental and analysis methods, and that may restrict their application to real-world systems. It is quite possible to make highly precise but meaningless measurements! An often-assumed condition for electrocatalyst analysis is the absence of mass transport limitation. For some reactions, such as the acidic hydrogen oxidation and hydrogen evolution reactions, this state is arguably so challenging to reach at representative conditions that it is impossible to measure true catalyst activity 11 . For example, ex situ thin-film rotating disk electrode measurements routinely fail to predict correct trends in catalyst performance in morphologically complex catalyst layers  as relevant operating conditions (e.g. meaningful current densities) are theoretically inaccessible. This topic has been extensively discussed with some authors directly criticising this technique and exploring alternatives 37 , 38 , and others defending the technique’s applicability for ranking catalysts if scrupulous attention is paid to experimental details 39 ; yet, many reports continue to use this measurement technique blindly with no regard for its applicability. We therefore strongly urge those planning measurements to consider whether their chosen technique is capable of providing sufficient evidence to disprove their hypothesis, even if it has been widely used for similar experiments.

The correct choice of technique should be dependent upon the measurand being probed rather than simply following previous reports. The case of iR correction, where a measurement of the uncompensated resistance is used to correct the applied voltage, is a good example. When the measurand is a material property, such as intrinsic catalyst activity, the uncompensated resistance is a source of error introduced by the experimental method and it should carefully be corrected out (Fig.  1 ). In the case that the uncompensated resistance is intrinsic to the measurand—for instance the operating voltage of an electrolyser cell—iR compensation is inappropriate and only serves to obfuscate. Another example is the choice of ex situ (outside the operating environment), in situ (in the operating environment), and operando (during operation) measurements. While in situ or operando testing allows characterisation under conditions that are more representative of real-world use, it may also yield measurements with increased uncertainty due to the decreased possibility for fine experimental control. Depending on the intended use of the measurement, an informed compromise must be sought between how relevant and how uncertain the resulting measurement will be.

Maximising reproducibility

Most electrochemists assess the repeatability of measurements, performing the same measurement themselves several times. Repeats, where all steps (including sample preparation, where relevant) of a measurement are carried out multiple times, are absolutely crucial for highlighting one-off mistakes (Fig.  2 ). Reproducibility, however, is assessed when comparing results reported by different laboratories. Many readers will be familiar with the variability in key properties reported for various systems e.g. variability in the reported electrochemically active surface area (ECSA) of commercial catalysts, which might reasonably be expected to be constant, suggesting that, in practice, the reproducibility of results cannot be taken for granted. As electrochemistry deals mostly with method-defined measurands, the measurement procedure must be standardised for results to be comparable. Variation in results therefore strongly suggests that measurements are not being performed consistently and that the information typically supplied when publishing experimental methods is insufficient to facilitate reproducibility of electrochemical measurements. Quantitative electrochemical measurements require control over a large range of parameters, many of which are easily overlooked or specified imprecisely when reporting data. An understanding of the crucial parameters and methods for their control is often institutional knowledge, held by expert electrochemists, but infrequently formalised and communicated e.g. through publication of widely adopted standards. This creates challenges to both reproducibility and the corresponding assessment of experimental quality by reviewers. The reporting standards established by various publishers (see Introduction) offer a practical response, but it is still unclear whether these will contain sufficiently granular detail to improve the situation.

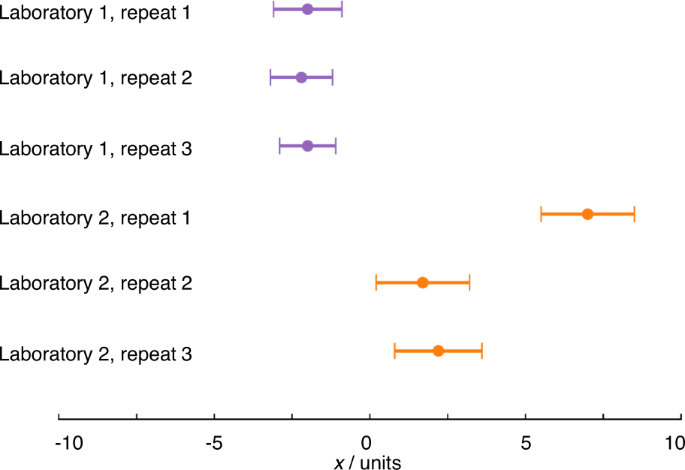
The measurements from laboratory 1 show a high degree of repeatability, while the measurements from laboratory 2 do not. Apparently, a mistake has been made in repeat 1, which will need to be excluded from any analysis and any uncertainty analysis, and/or suggests further repeat measurements should be conducted. The error bars are based on an uncertainty with coverage factor ~95% (see below) so the results from the two laboratories are different, i.e. show poor reproducibility. This may indicate differing experimental practice or that some as yet unidentified parameter is influencing the results.

Besides information typically supplied in the description of experimental methods for publication, which, at a minimum, must detail the materials, equipment and measurement methods used to generate the results, we suggest that a much more comprehensive description is often required, especially where measurements have historically poor reproducibility or the presented results differ from earlier reports. Such an expanded ‘supplementary experimental’ section would additionally include any details that could impact the results: for example, material pre-treatment, detailed electrode preparation steps, cleaning procedures, expected electrolyte and gas impurities, electrode preconditioning processes, cell geometry including electrode positions, detail of junctions between electrodes, and any other fine experimental details which might be institutional knowledge but unknown to the (now wide) readership of the electrochemical literature. In all cases any corrections and calculations used should be specified precisely and clearly justified; these may include determinations of properties of the studied system, such as ECSA, or of the environment, such as air pressure. We highlight that knowledge of the ECSA is crucial for conventional reporting of intrinsic electrocatalyst activity, but is often very challenging to measure in a reproducible manner 40 , 41 .

To aid reproducibility we recommend regularly calibrating experimental equipment and doing so in a way that is traceable to primary standards realising the International System of Units (SI) base units. The SI system ensures that measurement units (such as the volt) are uniform globally and invariant over time. Calibration applies to direct experimental indicators, e.g. loads and potentiostats, but equally to supporting tools such as temperature probes, balances, and flow meters. Calibration of reference electrodes is often overlooked even though variations from ideal behaviour can be significant 42 and, as discussed above, are often the limit of accuracy on potential measurement. Sometimes reports will specify internal calibration against a known reaction (such as the onset of the hydrogen evolution reaction), but rarely detail regular comparisons to a local master electrode artefact such as a reference hydrogen electrode or explain how that artefact is traceable, e.g. through control of the filling solution concentration and measurement conditions. If reference is made to a standardised material (e.g. commercial Pt/C) the specified material should be both widely available and the results obtained should be consistent with prior reports.

Beyond calibration and reporting, the best test of reproducibility is to perform intercomparisons between laboratories, either by comparing results to identical experiments reported in the literature or, more robustly, through participation in planned intercomparisons (for example ‘round-robin’ exercises); we highlight a recent study applied to solid electrolyte characterisation as a topical example 43 . Intercomparisons are excellent at establishing the key features of an experimental method and the comparability of results obtained from different methods; moreover they provide a consensus against which other laboratories may compare themselves. However, performing repeat measurements for assessing repeatability and reproducibility cannot estimate uncertainty comprehensively, as it excludes systematic sources of uncertainty.

Assessing measurement uncertainty

Formal uncertainty evaluation is an alien concept to most electrochemists; even the best papers (as well as our own!) typically report only the standard deviation between a few repeats. Metrological best practice dictates that reported values are stated as the combination of a best estimate of the measurand, and an interval, and a coverage factor ( k ) which gives the probability of the true value being within that interval. For example, “the turnover frequency of the electrocatalyst is 1.0 ± 0.2 s −1 ( k  = 2)” 16 means that the scientist (having assumed normally distributed error) is 95% confident that the turnover frequency lies in the range 0.8–1.2 s −1 . Reporting results in such a way makes it immediately clear whether the measurements reliably support the stated conclusions, and enables meaningful comparisons between independent results even if their uncertainties differ (Fig.  3 ). It also encourages honesty and self-reflection about the shortcomings of results, encouraging the development of improved experimental techniques.

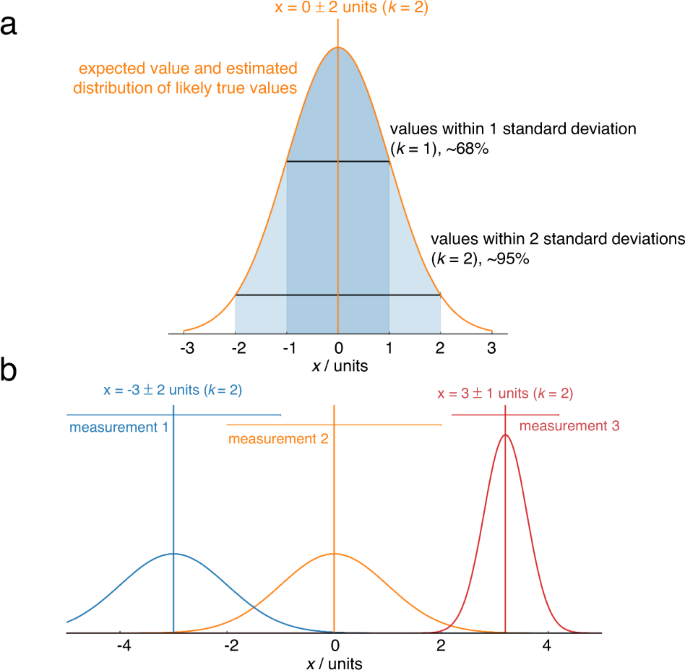
a Complete reporting of a measurement includes the best estimate of the measurand and an uncertainty and the probability the true value falls within the uncertainty reported. Here, the percentages indicate that a normal distribution has been assumed. b Horizontal bars indicate 95% confidence intervals from uncertainty analysis. The confidence intervals of measurements 1 and 2 overlap when using k  = 2, so it is not possible to say with 95% confidence that the result of the measurement 2 is higher than measurement 1, but it is possible to say this with 68% confidence, i.e. k  = 1. Measurement 3 has a lower uncertainty, so it is possible to say with 95% confidence that the value is higher than measurement 2.

Constructing such a statement and performing the underlying calculations often appears daunting, not least as there are very few examples for electrochemical systems, with pH measurements being one example to have been treated thoroughly 44 . However, a standard process for uncertainty analysis exists, as briefly outlined graphically in Fig.  4 . We refer the interested reader to both accessible introductory texts 45 and detailed step-by-step guides 16 , 46 . The first steps in the process are to state precisely what is being measured—the measurand—and identify likely sources of uncertainty. Even this qualitative effort is often revealing. Precision in the definition of the measurand (and how it is determined from experimental indicators) clarifies the selection of measurement technique and helps to assess its appropriateness; for example, where the measurand relates only to an instantaneous property of a specific physical object, e.g. the current density of a specific fuel cell at 0.65 V following a standardised protocol, we ignore all variability in construction, device history etc. and no error is introduced by the sample. Whereas, when the measurand is a material property, such as turnover frequency of a catalyst material with a defined chemistry and preparation method, variability related to the material itself and sample preparation will often introduce substantial uncertainty in the final result. In electrochemical measurements, errors may arise from a range of sources including the measurement equipment, fluctuations in operating conditions, or variability in materials and samples. Identifying these sources leads to the design of better-quality experiments. In essence, the subsequent steps in the calculation of uncertainty quantify the uncertainty introduced by each source of error and, by using a measurement model or a sensitivity analysis (i.e. an assessment of how the results are sensitive to variability in input parameters), propagate these to arrive at a final uncertainty on the reported result.

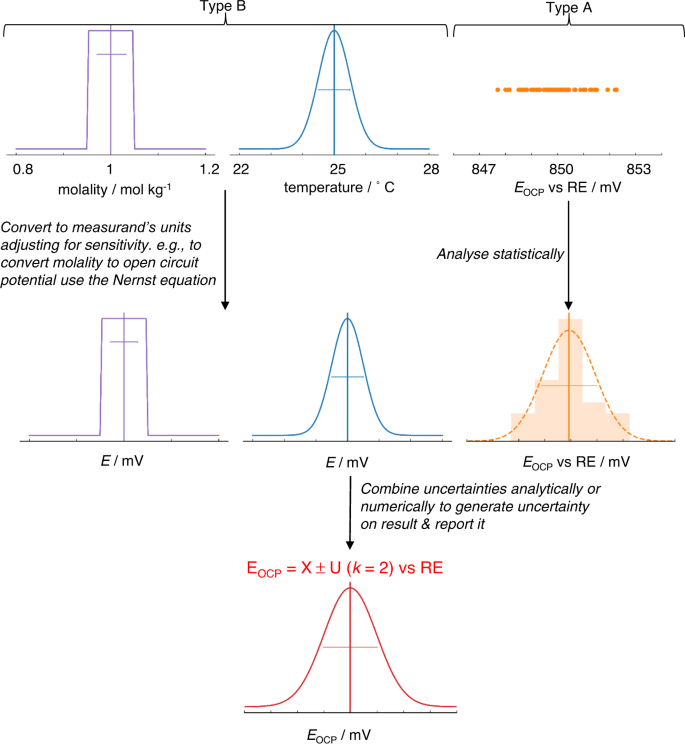
Possible sources of uncertainty are identified, and their standard uncertainty or probability distribution is determined by statistical analysis of repeat measurements (Type A uncertainties) or other evidence (Type B uncertainties). If required, uncertainties are then converted into the same unit as the measurand and adjusted for sensitivity, using a measurement model. Uncertainties are then combined either analytically using a standard approach or numerically to generate an overall estimate of uncertainty for the measurand (as indicated in Fig.  3a ).

Generally, given the historically poor understanding of uncertainty in electrochemistry, we promote increased awareness of uncertainty reporting standards and a focus on reporting measurement uncertainty with a level of detail that is appropriate to the claim made, or the scientific utilisation of the data. For example, where the primary conclusion of a paper relies on demonstrating that a material has the ‘highest ever X’ or ‘X is bigger than Y’ it is reasonable for reviewers to ask authors to quantify how confident they are in their measurement and statement. Additionally, where uncertainties are reported, even with error bars in numerical or graphical data, the method by which the uncertainty was determined should be stated, even if the method is consciously simple (e.g. “error bars indicate the sample standard deviation of n  = 3 measurements carried out on independent electrodes”). Unfortunately, we are aware of only sporadic and incomplete efforts to create formal uncertainty budgets for electrochemical measurements of energy technologies or materials, though work is underway in our group to construct these for some exemplar systems.

Electrochemistry has undoubtedly thrived without significant interaction with formal metrology; we do not urge an abrupt revolution whereby rigorous measurements become devalued if they lack additional arcane formality. Rather, we recommend using the well-honed principles of metrology to illuminate best practice and increase transparency about the strengths and shortcomings of reported experiments. From rethinking experimental design, to participating in laboratory intercomparisons and estimating the uncertainty on key results, the application of metrological principles to electrochemistry will result in more robust science.

Climent, V. & Feliu, J. M. Thirty years of platinum single crystal electrochemistry. J. Solid State Electrochem . https://doi.org/10.1007/s10008-011-1372-1 (2011).

Nature Editors and Contributors. Challenges in irreproducible research collection. Nature https://www.nature.com/collections/prbfkwmwvz/ (2018).

Chen, J. G., Jones, C. W., Linic, S. & Stamenkovic, V. R. Best practices in pursuit of topics in heterogeneous electrocatalysis. ACS Catal. 7 , 6392–6393 (2017).

Article   CAS   Google Scholar  

Voiry, D. et al. Best practices for reporting electrocatalytic performance of nanomaterials. ACS Nano 12 , 9635–9638 (2018).

Article   CAS   PubMed   Google Scholar  

Wei, C. et al. Recommended practices and benchmark activity for hydrogen and oxygen electrocatalysis in water splitting and fuel cells. Adv. Mater. 31 , 1806296 (2019).

Article   Google Scholar  

Chem Catalysis Editorial Team. Chem Catalysis Checklists Revision 1.1 . https://info.cell.com/introducing-our-checklists-learn-more (2021).

Chatenet, M. et al. Good practice guide for papers on fuel cells and electrolysis cells for the Journal of Power Sources. J. Power Sources 451 , 227635 (2020).

Sun, Y. K. An experimental checklist for reporting battery performances. ACS Energy Lett. 6 , 2187–2189 (2021).

Li, J. et al. Good practice guide for papers on batteries for the Journal of Power Sources. J. Power Sources 452 , 227824 (2020).

Arbizzani, C. et al. Good practice guide for papers on supercapacitors and related hybrid capacitors for the Journal of Power Sources. J. Power Sources 450 , 227636 (2020).

Hansen, J. N. et al. Is there anything better than Pt for HER? ACS Energy Lett. 6 , 1175–1180 (2021).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Xu, K. Navigating the minefield of battery literature. Commun. Mater. 3 , 1–7 (2022).

Dix, S. T., Lu, S. & Linic, S. Critical practices in rigorously assessing the inherent activity of nanoparticle electrocatalysts. ACS Catal. 10 , 10735–10741 (2020).

Mistry, A. et al. A minimal information set to enable verifiable theoretical battery research. ACS Energy Lett. 6 , 3831–3835 (2021).

Joint Committee for Guides in Metrology: Working Group 2. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms . (2012).

Joint Committee for Guides in Metrology: Working Group 1. Evaluation of measurement data—Guide to the expression of uncertainty in measurement . (2008).

International Organization for Standardization: Committee on Conformity Assessment. ISO 17034:2016 General requirements for the competence of reference material producers . (2016).

Brown, R. J. C. & Andres, H. How should metrology bodies treat method-defined measurands? Accredit. Qual. Assur . https://doi.org/10.1007/s00769-020-01424-w (2020).

Angerstein-Kozlowska, H. Surfaces, Cells, and Solutions for Kinetics Studies . Comprehensive Treatise of Electrochemistry vol. 9: Electrodics: Experimental Techniques (Plenum Press, 1984).

Shinozaki, K., Zack, J. W., Richards, R. M., Pivovar, B. S. & Kocha, S. S. Oxygen reduction reaction measurements on platinum electrocatalysts utilizing rotating disk electrode technique. J. Electrochem. Soc. 162 , F1144–F1158 (2015).

International Organization for Standardization: Technical Committee ISO/TC 197. ISO 14687:2019(E)—Hydrogen fuel quality—Product specification . (2019).

Schmidt, T. J., Paulus, U. A., Gasteiger, H. A. & Behm, R. J. The oxygen reduction reaction on a Pt/carbon fuel cell catalyst in the presence of chloride anions. J. Electroanal. Chem. 508 , 41–47 (2001).

Chen, R. et al. Use of platinum as the counter electrode to study the activity of nonprecious metal catalysts for the hydrogen evolution reaction. ACS Energy Lett. 2 , 1070–1075 (2017).

Ji, S. G., Kim, H., Choi, H., Lee, S. & Choi, C. H. Overestimation of photoelectrochemical hydrogen evolution reactivity induced by noble metal impurities dissolved from counter/reference electrodes. ACS Catal. 10 , 3381–3389 (2020).

Jerkiewicz, G. Applicability of platinum as a counter-electrode material in electrocatalysis research. ACS Catal. 12 , 2661–2670 (2022).

Guo, J., Hsu, A., Chu, D. & Chen, R. Improving oxygen reduction reaction activities on carbon-supported ag nanoparticles in alkaline solutions. J. Phys. Chem. C. 114 , 4324–4330 (2010).

Arulmozhi, N., Esau, D., van Drunen, J. & Jerkiewicz, G. Design and development of instrumentations for the preparation of platinum single crystals for electrochemistry and electrocatalysis research Part 3: Final treatment, electrochemical measurements, and recommended laboratory practices. Electrocatal 9 , 113–123 (2017).

Colburn, A. W., Levey, K. J., O’Hare, D. & Macpherson, J. V. Lifting the lid on the potentiostat: a beginner’s guide to understanding electrochemical circuitry and practical operation. Phys. Chem. Chem. Phys. 23 , 8100–8117 (2021).

Ban, Z., Kätelhön, E. & Compton, R. G. Voltammetry of porous layers: staircase vs analog voltammetry. J. Electroanal. Chem. 776 , 25–33 (2016).

McMath, A. A., Van Drunen, J., Kim, J. & Jerkiewicz, G. Identification and analysis of electrochemical instrumentation limitations through the study of platinum surface oxide formation and reduction. Anal. Chem. 88 , 3136–3143 (2016).

Jerkiewicz, G. Standard and reversible hydrogen electrodes: theory, design, operation, and applications. ACS Catal. 10 , 8409–8417 (2020).

Ives, D. J. G. & Janz, G. J. Reference Electrodes, Theory and Practice (Academic Press, 1961).

Newman, J. & Balsara, N. P. Electrochemical Systems (Wiley, 2021).

Inzelt, G., Lewenstam, A. & Scholz, F. Handbook of Reference Electrodes (Springer Berlin, 2013).

Cimenti, M., Co, A. C., Birss, V. I. & Hill, J. M. Distortions in electrochemical impedance spectroscopy measurements using 3-electrode methods in SOFC. I—effect of cell geometry. Fuel Cells 7 , 364–376 (2007).

Hoshi, Y. et al. Optimization of reference electrode position in a three-electrode cell for impedance measurements in lithium-ion rechargeable battery by finite element method. J. Power Sources 288 , 168–175 (2015).

Article   ADS   CAS   Google Scholar  

Jackson, C., Lin, X., Levecque, P. B. J. & Kucernak, A. R. J. Toward understanding the utilization of oxygen reduction electrocatalysts under high mass transport conditions and high overpotentials. ACS Catal. 12 , 200–211 (2022).

Masa, J., Batchelor-McAuley, C., Schuhmann, W. & Compton, R. G. Koutecky-Levich analysis applied to nanoparticle modified rotating disk electrodes: electrocatalysis or misinterpretation. Nano Res. 7 , 71–78 (2014).

Martens, S. et al. A comparison of rotating disc electrode, floating electrode technique and membrane electrode assembly measurements for catalyst testing. J. Power Sources 392 , 274–284 (2018).

Wei, C. et al. Approaches for measuring the surface areas of metal oxide electrocatalysts for determining their intrinsic electrocatalytic activity. Chem. Soc. Rev. 48 , 2518–2534 (2019).

Lukaszewski, M., Soszko, M. & Czerwiński, A. Electrochemical methods of real surface area determination of noble metal electrodes—an overview. Int. J. Electrochem. Sci. https://doi.org/10.20964/2016.06.71 (2016).

Niu, S., Li, S., Du, Y., Han, X. & Xu, P. How to reliably report the overpotential of an electrocatalyst. ACS Energy Lett. 5 , 1083–1087 (2020).

Ohno, S. et al. How certain are the reported ionic conductivities of thiophosphate-based solid electrolytes? An interlaboratory study. ACS Energy Lett. 5 , 910–915 (2020).

Buck, R. P. et al. Measurement of pH. Definition, standards, and procedures (IUPAC Recommendations 2002). Pure Appl. Chem. https://doi.org/10.1351/pac200274112169 (2003).

Bell, S. Good Practice Guide No. 11. The Beginner’s Guide to Uncertainty of Measurement. (Issue 2). (National Physical Laboratory, 2001).

United Kingdom Accreditation Service. M3003 The Expression of Uncertainty and Confidence in Measurement  4th edn. (United Kingdom Accreditation Service, 2019).

Download references

Acknowledgements

This work was supported by the National Measurement System of the UK Department of Business, Energy & Industrial Strategy. Andy Wain, Richard Brown and Gareth Hinds (National Physical Laboratory, Teddington, UK) provided insightful comments on the text.

Author information

Authors and affiliations.

National Physical Laboratory, Hampton Road, Teddington, TW11 0LW, UK

Graham Smith & Edmund J. F. Dickinson

You can also search for this author in PubMed   Google Scholar

Contributions

G.S. originated the concept for the article. G.S. and E.J.F.D. contributed to drafting, editing and revision of the manuscript.

Corresponding author

Correspondence to Graham Smith .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature Communications thanks Gregory Jerkiewicz for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Smith, G., Dickinson, E.J.F. Error, reproducibility and uncertainty in experiments for electrochemical energy technologies. Nat Commun 13 , 6832 (2022). https://doi.org/10.1038/s41467-022-34594-x

Download citation

Received : 29 July 2022

Accepted : 31 October 2022

Published : 11 November 2022

DOI : https://doi.org/10.1038/s41467-022-34594-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Electrochemical surface-enhanced raman spectroscopy.

• Christa L. Brosseau
• Alvaro Colina

Nature Reviews Methods Primers (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

What are some common mistakes students make with galvanic cells?

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

Galvanic Cell - lab report

Organic chemistry ii (chem 3412), augusta university, students also viewed.

• Experiment 10 oxidation-reduction reactions 519
• 04 acetal 367 131 - lab report
• Exp - lab report
• Unknown Solution-VM10
• CHM12 Experiment 4 Gas Chromatography 1
• 6 Alcohols and Phenols - lab report

Related documents

• Soap - Lab report
• Acid Base Titration - lab report
• 2423L5 - Lab report
• Extraction of Caffeine from Energy Drinks
• Forensic Analysis of an Analgesic
• Ex. 8 - Synthesis of t-Amyl Chloride (2020)

Preview text

Experiment 9, electrochemistry i – galvanic cell.

Introduction: Chemical reactions involving the transfer of electrons from one reactant to another are called oxidation-reduction reactions or redox reactions. In a redox reaction, two half-reactions occur; one reactant gives up electrons (undergoes oxidation) and another reactant gains electrons (undergoes reduction). A piece of zinc going into a solution as zinc ions, with each Zn atom giving up 2 electrons, is an example of an oxidation half-reaction.

Zn( s ) → Zn2+( aq ) + 2e- (1)

The oxidation number of Zn( s ) is 0 and the oxidation number of the Zn2+ is +2. Therefore, in this half-reaction, the oxidation number increases , which is another way of defining an oxidation. In contrast, the reverse reaction, in which Zn2+ ions gain 2 electrons to become Zn atoms, is an example of reduction.

Zn2+( aq ) + 2e- → Zn( s ) (2)

In a reduction there is a decrease (or reduction) in oxidation number. Chemical equation representing half-reactions must be both mass and charge balanced. In the half-reactions above, there is one zinc on both sides of the equation. The charge is balanced because the 2+ charge on the zinc ion is balanced by two electrons, 2e-, giving zero net charge on both sides.

Another example of reduction is the formation of solid copper from copper ions in solution.

Cu2+( aq ) + 2e- → Cu( s ) (3)

In this half-reaction the oxidation number of the aqueous copper is +2, which decreases to 0 for the solid copper, and again charge and mass are balanced. However, no half-reaction can occur by itself. A redox reaction results when an oxidation and a reduction half-reaction are combined to complete a transfer of electrons as in the following example:

Zn( s ) + Cu2+( aq ) → Zn2+( aq ) + Cu( s ) (4)

The electrons are not shown because they are neither reactants nor products but have simply been transferred from one species to another (from Zn to Cu2+ in this case). In this redox reaction, the Zn( s ) is referred to as the reducing agent because it causes the Cu2+ to be reduced to Cu. The Cu2+ is called the oxidizing agent because it causes the Zn( s ) to be oxidized to Zn2+.

Any half-reaction can be expressed as a reduction as illustrated in the case where equation (1) can be reversed to equation (2). A measure of the tendency for a reduction to occur is its reduction potential , E, measured in units of volts . At standard conditions, 25 °C and concentrations of 1 M for the aqueous ions, the measured voltage of the reduction half- reaction is defined as the standard reduction potential , E °**.** Standard reduction potentials

have been measured for many half-reactions and they are listed in tables. A short list is also provided at the end of the In-Lab section. For the reduction half-reactions in equations (2) and (3), the standard reduction potentials are –0 V for zinc and +0 V for copper. The more positive (or less negative) the reduction potential, the greater is the tendency for the reduction to occur. So Cu2+ has a greater tendency to be reduced than Zn2+. Furthermore, Zn has a greater tendency to be oxidized than Cu. The values of E ° for the oxidation half- reactions are opposite in sign to the reduction potentials: +0 V for Zn and –0 V for Cu.

A galvanic cell or voltaic cell is a device in which a redox reaction, such as the one in equation (4), spontaneously occurs and produces an electric current. In order for the transfer of electrons in a redox reaction to produce an electric current and be useful, the electrons are made to pass through an external electrically conducting wire instead of being directly transferred between the oxidizing and reducing agents. The design of a galvanic cell (shown in Figure 1 for the equation (4) reaction) allows this to occur. In a galvanic cell, two solutions, one containing the ions of the oxidation half-reaction and the other containing the ions of the reduction half-reaction, are placed in separated compartments called half-cells . For each half-cell, the metal, which is called an electrode , is placed in the solution and connected to an external wire. The electrode at which oxidation occurs is called the anode [Zn in equation (4)] and the electrode at which reduction occurs is called the cathode [Cu in equation (4)]. The two half-cells are connected by a salt-bridge that allows a “current” of ions from one half-cell to the other to complete the circuit of electron current in the external wires. When the two electrodes are connected to an electric load (such as a light bulb or voltmeter) the circuit is completed, the oxidation-reduction reaction occurs, and electrons move from the anode (−) to the cathode (+), producing an electric current.

Figure 1. Galvanic cell (or battery) based on the redox reaction in equation (4).

The cell potential , E cell, which is a measure of the voltage that the battery can provide, is calculated from the half-cell reduction potentials:

E cell = E cathode - E anode

Thus a plot such as the one shown below can be generated by measuring the cell potential for different values of [Cu2+], while keeping [Zn2+] constant (at 1 M in this plot). The equation of the line in this plot can then be used to determine ln [Cu2+] in a solution of unknown concentration from its measured E cell, as long as [Zn2+] remains at 1 M and the temperature at 25oC. This is the same principle used in a pH meter for the determination of [H+]. Notice that as the concentration of Cu2+ ion reactant increases (or ln[Cu2+] becomes less negative), the potential of the cell increases.

Nernst plot: Zn( s )|Zn2+||C u2+|C u( s ) ([Zn2+] a t 1 M )

-14 -12 -10 -8 -6 -4 -2 0. ln[Cu2+]

Figure 2. Nernst plot of E cell vs. ln [Cu2+] with [Zn2+] constant at 1 M . Note the standard cell notation in the graph title for the galvanic cell.

Part A. Redox Reactions: In this experiment you will observe several redox reactions in which metals are placed in solutions containing different metal ions. From your observations you will determine whether a redox reaction is occurring and write balanced redox equations for any that occur. For example, since as shown above, Cu2+ has a greater tendency to be reduced than Zn2+, you would expect that placing Zn metal into a solution of Cu2+ ions would result in a direct redox reaction. Cu2+ ions are reduced to Cu metal which is deposited on the Zn metal surface, while the Zn metal is oxidized to Zn 2+ ions which go into the solution. The redox equation for this reaction is therefore equation (4).

Part B: Reduction Potentials: You will then construct a series of three galvanic cells combining the zinc half-reaction with three different metal half-reactions (Cu, Fe and Pb). You will measure the cell potentials, E °cell, using a Vernier voltage probe as shown in Figure 3. You will use 1 M solutions for both half-cells, so Q = 1 and lnQ = 0 for the reaction. Thus the cell potential measured will be the same as E °cell as evident from the Nernst equation (6). You will then use your

measured E °cell values, the known zinc standard reduction potential, E ° = –0 V, and equation (5) to calculate the E ° values for the three different half-reactions.

Part C: Nernst Equation for varying Cu2+ concentrations: Galvanic cells with different known Cu2+ concentrations and a fixed Zn2+ concentration will be prepared and their cell potentials measured. A plot of the Nernst equation, E cell vs. ln[Cu2+], constructed from this data will then be used to find [Cu2+] of an unknown solution.

Part D: Determine the E ° for a voltaic cell using Cu and unknown metal: Finally, you will measure the potential of a voltaic cell combining an unknown metal electrode with Cu ( E ° = 0 V). By measurement of the cell potential and use of equation (5), you will identify the unknown metal from its calculated value of E °. The unknown will have a more negative E ° than Cu, so the Cu will have a greater tendency to be reduced and thus will be the cathode when the E °cell is positive.

Pre-Lab Notebook: Provide a title, purpose, and a brief summary of the procedure in your lab notebook before coming to lab.

12-Well Microcell plate Vernier LabPro 24-Well Microcell plate TI-84 Calculator 1 mL Pipet Vernier Voltage Probe Pipet bulb Steel Wool 50 mL Beakers (5) Filter paper strips Forceps 100 mL Volumetric flasks (3)

In Lab Procedure: Note: Work in pairs

Part A. Redox Reactions: 1. Fill four cells in each of four columns of a 24-well microcell plate about three-fourths full with 1 M Cu(NO 3 ) 2 , 1 M FeSO 4 , 1 M Pb(NO 3 ) 2 , and 1 M Zn(NO 3 ) 2 as shown in the diagram below. 2. Polish small strips (4 each) of Cu, Fe, Pb and Zn with steel wool or sand paper and place them on a paper towel with written labels to insure that the metals are not mixed up with each other. Partially submerge the strips into the cell rows as shown below. Place only part of the metal into the solution so that any sign of a reaction (such as deposit of a metal on the submerged part of the strip) can be determined by comparison with the unsubmerged portion of the metal strip.

Cu(NO 3 ) 2 FeSO 4 Pb(NO 3 ) 2 Zn(NO 3 ) 2 Cu( s ) Fe( s ) Pb( s ) Zn( s )

• Record the positive cell potential, in volts, in your laboratory notebook. You will find that the voltage recorded is less than what you would expect based on standard reduction potentials. For example the Zn/Cu cell may be less than the 1 V calculated in the Introduction section. This is partly due to the presence of an oxide formed on one of the electrodes, a process which occurs very rapidly for easily oxidized metals and which changes the half-cell potential.
• Repeat steps 3-6 for galvanic cells of Fe(in 1 M FeSO 4 ) - Zn and Pb(in 1 M Pb(NO 3 ) 2 ) - Zn. Use a freshly prepared filter paper strip for the salt bridge of each cell.

Part C: Nernst Equation for varying Cu2+ concentrations:

• Prepare three dilute solutions of CuSO 4 by serial dilution from a 1 M CuSO 4 stock solution as follows: Transfer1 mL of 1 M CuSO 4 stock solution into a labeled (with tape) 100 mL volumetric flask and dilute to the mark with de-ionized water to form a 0 M solution. Rinse the pipet with a small volume of the solution to be transferred prior to use. Next take the 0 M solution just formed and transfer 1 mL of it into a labeled 100 mL volumetric flask. Dilute to the mark with de-ionized water to form the 0 M solution. Repeat one more time so that you have the following set of solutions in labeled flasks: Solution A – 1 M CuSO 4 (stock solution) Solution B – 0 M CuSO 4 Solution C – 0 M CuSO 4 Solution D – 0 M CuSO 4
• Prepare a half-cell of Cu2+ by placing the copper solution D into a 12-microcell well.
• Remove the copper and zinc electrodes from the half-cells used previously and clean and re-polish them.
• Place 1 M Zn(NO 3 ) 2 in a cell next to the Cu2+ half-cell. Connect the two half-cells with a freshly prepared salt bridge. Connect the copper and zinc electrodes to the correct voltage probe leads. Measure and record the cell potential in your laboratory notebook using the same technique (5-10 second immersion) with the voltage probe as in Part B.
• Remove the CuSO 4 solution with a disposable pipet and repeat the measurement of E cell (steps 3-4) for the remaining three copper solutions in order of increasing concentration. Then, in the same way, measure the E cell for the unknown Cu2+ solution. Record the measured values in a table as shown below in your notebook.

Solution D C B A Unknown [Cu2+] 0 M 0 M 0 M 1 M ? Volts

Part D: Determine the E ° for a voltaic cell using Cu and unknown metal: 1 1. Obtain a small amount of the unknown electrolyte solution labeled “1 M X ion” and the corresponding metal strip, “X”. This metal is one of the metals in the table of Standard Reduction Potentials at the end of the In-Lab section. 2. Use a disposable pipet to transfer a small amount of 1 M X ion solution to a well adjacent to the 1 M CuSO 4 solution in a 12-microcell-test plate. 3. Make a new salt bridge by soaking a short length of filter paper in the KNO 3 solution. 4. Connect the X and Cu half-cells with the filter paper. Measure the positive potential of the X-Cu voltaic cell using the same technique as in Part B ( Red lead to the Cu , which is the cathode).

• After recording the potential once (5-10 seconds), remove both electrodes from the solutions and clean and polish each electrode. Set up the galvanic cell again. Connect the voltage probe as before.
• Record the potential again. If the two measured potentials do not agree within. volts, test the galvanic cell a third time and record the potential immediately after making the connection with the voltage probe. Calculate the average of the measured potentials to use in the Post-Lab calculation.

Standard Reduction Potentials:

Electrode E o

Ag+ + e− → Ag +0 V

Cu2+ + 2e− → Cu +0 V

Pb2+ + 2e− → Pb −0

Fe2+ + 2e− → Fe −0 V

Zn2+ + 2e− → Zn −0 V

Al3+ + 3e− → Al −1 V

Mg2+ + 2e− → Mg −2 V

Literature Cited:

• Advanced Chemistry with Vernier: Experiments for AP, IB, and College General Chemistry , Jack Randall, Vernier Software and Technology , 2004, 20-1.
• Multiple Choice

Course : Organic Chemistry II (CHEM 3412)

University : augusta university.

• Discover more from: Organic Chemistry II CHEM 3412 Augusta University 298   Documents Go to course
• More from: Organic Chemistry II CHEM 3412 Augusta University 298   Documents Go to course